题目内容
9.一次函数y=3x-2的图象与坐标轴围成的三角形的面积是$\frac{2}{3}$.分析 先根据坐标轴上点的坐标特征求出直线与坐标轴的交点坐标,然后根据三角形面积公式求解.
解答 解:当x=0时,y=3x-2=-2,则直线与y轴的交点坐标为(0,-2);
当y=0时,3x-2=0,解得x=$\frac{2}{3}$,则直线与x轴的交点坐标为($\frac{2}{3}$,0),
所以函数y=3x-2的图象与坐标轴围成的三角形面积=$\frac{1}{2}$×2×$\frac{2}{3}$=$\frac{2}{3}$.
故答案为$\frac{2}{3}$.
点评 本题考查了一次函数图象上点的坐标特征:直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
19. 如图是一个正方体展开图,把展开图折叠成正方体后,“遵”字一面的相对面上的字是( )
如图是一个正方体展开图,把展开图折叠成正方体后,“遵”字一面的相对面上的字是( )
 如图是一个正方体展开图,把展开图折叠成正方体后,“遵”字一面的相对面上的字是( )
如图是一个正方体展开图,把展开图折叠成正方体后,“遵”字一面的相对面上的字是( )| A. | 交 | B. | 通 | C. | 条 | D. | 例 |

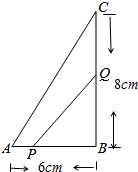 如图,△ABC中,∠B=90°,点P从A点开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,当一方停止运动时另一方也随之停止运动.
如图,△ABC中,∠B=90°,点P从A点开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,当一方停止运动时另一方也随之停止运动. 如图,△ABC的内切圆⊙O与三边分别相切于D、E、F三点,AB=7,BC=12,CA=11,
如图,△ABC的内切圆⊙O与三边分别相切于D、E、F三点,AB=7,BC=12,CA=11,