题目内容
如图7,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H。
(1)求证:△EAB≌△GAD;
(2)若AB=3 ,AG=3,求EB的长。
,AG=3,求EB的长。
 |
图7
(1)证明:∵四边形ABCD、AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG,
∴∠EAB=∠GAD,
在△AEB和△AGD中,
 ,
,
∴△EAB≌△GAD(SAS);
(2)∵△EAB≌△GAD,
∴EB=GD,
∵四边形ABCD是正方形,AB=3 ,
,
∴BD⊥AC,AC=BD= AB=6,
AB=6,
∴∠DOG=90°,OA=OD= BD=3,
BD=3,
∵AG=3,
∴OG=OA+AG=6,
∴GD= =3
=3 ,
,
∴EB=3 .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为区级先进班集体,下表是这三个班的五项素质考评得分表:
五项成绩素质考评得分(单位:分)
| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 甲班 | 10 | 10 | 6 | 10 | 7 |
| 乙班 | 10 | 8 | 8 | 9 | 8 |
| 丙班 | 9 | 10 | 9 | 6 | 9 |
根据统计表中的信息解答下列问题:
(1)请你补全五项成绩考评分析表中的数据:
五项成绩考评比较分析表(单位:分)
| 班级 | 平均数 | 众数 | 中位数 |
| 甲班 | 8.6 | 10 | |
| 乙班 | 8.6 | 8 | |
| 丙班 | 9 | 9 |
(2)参照表中的数据,你推荐哪个班为区级先进班集体?并说明理由; _________
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照按3:2:1:1:3的比确定,学生处的李老师根据这个平均成绩,绘制了一幅不完整的条形统计图,请将这个统计图补充完整,依照这个成绩,应推荐哪个班为市级先进班集体?

 B.
B. C.
C. D.
D.

 B.
B. C.
C. D.
D.

 ,0).点P是线段AB上一个动点(点P不与点A,B重合),过点P作AB的垂线分别与x轴交于点D,与y轴交于点E,DF平分∠PDO交y轴于点F.设点D的横坐标为t.
,0).点P是线段AB上一个动点(点P不与点A,B重合),过点P作AB的垂线分别与x轴交于点D,与y轴交于点E,DF平分∠PDO交y轴于点F.设点D的横坐标为t. 时,求证:DF∥CB;
时,求证:DF∥CB;  时,在图2中补全图形,判断直线DF与CB的位置关系,并证明你的结论;
时,在图2中补全图形,判断直线DF与CB的位置关系,并证明你的结论;  ,
,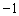 ),在点P运动的过程中,当△MCE的面积等于△BCO面积的
),在点P运动的过程中,当△MCE的面积等于△BCO面积的 倍时,直接写出此时点E的坐标.
倍时,直接写出此时点E的坐标. 


 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.