题目内容
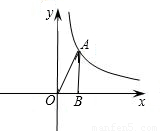
如图,第一象限内的点A在反比例函数 的图象上,且OA=
的图象上,且OA= ,OA与x轴正方向的夹角为α,tanα=
,OA与x轴正方向的夹角为α,tanα= ,
,
(1)求k的值,并求当y≤1时自变量x的取值范围;
(2)点B(m,-2)也在反比例函数 的图象上,连接AB,与x轴交于点C,若AC与x轴正方向的夹角为β,求sinβ的值;
的图象上,连接AB,与x轴交于点C,若AC与x轴正方向的夹角为β,求sinβ的值;
(3)点P在x轴上,且使得△OBP为直角三角形,则P点的坐标为______.

 解:(1)过A作AE⊥x轴于E,
解:(1)过A作AE⊥x轴于E,tan∠AOE=
 ,
,∴OE=3AE
∵OA=
 ,由勾股定理得:OE2+AE2=10,
,由勾股定理得:OE2+AE2=10,解得:AE=1,OE=3,
∴A的坐标为(3,1),
A点在双曲线上,
∴1=
 ,
,∴k=3,
当y≤1时,x≥3或x<0;
(2)B(m,-2)在双曲y=
 上,
上,∴-2=
 ,
,解得:m=-
 ,
,∴B的坐标是(-
 ,-2),
,-2),代入一次函数的解析式得:
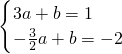 ,
,解得:
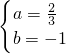 ,
,
∴一次函数的解析式为:y=
 x-1.
x-1.sinβ=
 ;
;(3)P(-
 ,0)或P(-
,0)或P(- ,0).
,0).分析:(1)过A作AE⊥x轴于E,由tan∠AOE=
 ,得到OE=3AE,根据勾股定理即可求出AE和OE的长,即得到A的坐标,代入双曲线即可求出k的值,得到解析式;
,得到OE=3AE,根据勾股定理即可求出AE和OE的长,即得到A的坐标,代入双曲线即可求出k的值,得到解析式;(2)把B的坐标代入反比例函数的解析式即可求出B的坐标,把A和B的坐标代入一次函数的解析式即可求出a、b的值,即得到答案.
(3)当BP⊥x轴,以及BP⊥y轴,分别求出即可.
点评:此题主要考查了锐角三角函数的定义,用待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,用待定系数法求正比例函数的解析式,正比例函数图象上点的坐标特征,勾股定理等知识点,综合运用这些知识进行计算是解此题的关键,题型较好,综合性比较强.

练习册系列答案
相关题目
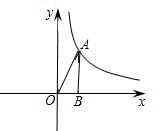 如图,第一象限内的点A在某反比例函数的图象上,过A作AB⊥x轴,垂足为B,连接AO,已知△AOB的面积为4.
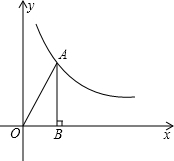
如图,第一象限内的点A在某反比例函数的图象上,过A作AB⊥x轴,垂足为B,连接AO,已知△AOB的面积为4. 如图:第一象限内的点A在一反比例函数图象上,过点A作AB⊥x轴,垂足为B点,连接AO,已知△AOB的面积为4.①求反比例函数的解析式;②若点A的纵坐标为4,过点A的直线与x轴相交于点P,且△APB与△AOB相似,求所有符合条件的点P的坐标;③在②的条件下,求过P、O、A的抛物线的顶点坐标.
如图:第一象限内的点A在一反比例函数图象上,过点A作AB⊥x轴,垂足为B点,连接AO,已知△AOB的面积为4.①求反比例函数的解析式;②若点A的纵坐标为4,过点A的直线与x轴相交于点P,且△APB与△AOB相似,求所有符合条件的点P的坐标;③在②的条件下,求过P、O、A的抛物线的顶点坐标.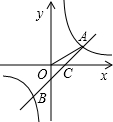
 已知△AOB的面积为4.
已知△AOB的面积为4.