题目内容
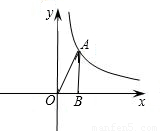
 如图:第一象限内的点A在一反比例函数图象上,过点A作AB⊥x轴,垂足为B点,连接AO,已知△AOB的面积为4.①求反比例函数的解析式;②若点A的纵坐标为4,过点A的直线与x轴相交于点P,且△APB与△AOB相似,求所有符合条件的点P的坐标;③在②的条件下,求过P、O、A的抛物线的顶点坐标.
如图:第一象限内的点A在一反比例函数图象上,过点A作AB⊥x轴,垂足为B点,连接AO,已知△AOB的面积为4.①求反比例函数的解析式;②若点A的纵坐标为4,过点A的直线与x轴相交于点P,且△APB与△AOB相似,求所有符合条件的点P的坐标;③在②的条件下,求过P、O、A的抛物线的顶点坐标.
分析:(1)求反比例函数的解析式实质求Y=
中K值,因为△AOB的面积为4,所以K=8;
(2)△APB与△AOB相似,可能全等,也可能相似,所以有三个点满足条件;
(3)欲求过P、O、A的抛物线的顶点坐标,先求其解析式,知道P、O、A三点坐标,用待定系数法易求,即解.
| K |
| X |
(2)△APB与△AOB相似,可能全等,也可能相似,所以有三个点满足条件;
(3)欲求过P、O、A的抛物线的顶点坐标,先求其解析式,知道P、O、A三点坐标,用待定系数法易求,即解.
解答:解:①设A(xA,yA)
∵
xAyA=4
∵XA>0,YA>0
∴xAyA=8
设y=
∴xAyA=k
∴k=8.
∴设比例函数解析式为y=
.(2分)
②∵yA=4,
∴xA=2
∴A(2,4)
∴OB=2,AB=4
当∠AP1B=∠AOB时,△AOB≌△APB
∴PB=OB=2,∴P1(4,0)(3分)
当∠AP2B=∠OAB时△AOB∽△P2AB
可以由
=
∴
=
BP2=8,∴P2(10,0).(4分)
当P3在x轴负半轴上时,
且P3与P2关于点B对称也满足△AOB∽△P3BA
由P2(10,0),B(2,0),
∴P3(-6,0).(5分)
③当抛物线经过P1(4,0),O(0,0),A(2,4)时
设解析式为y=ax2+bx+c
解
∴解析式为y=-x2+4x
∴顶点坐标是(2,4)(6分)
当抛物线经过P2(10,0),O(0,0),A(2,4)时
设所求抛物线为y=a2x2+b2x
则
∴y=-
x2+
x=-
(x-5)2+
∴顶点坐标是(5,
).(8分)
设经过P3(-6,0),O(0,0),A(2,4)的解析式为:y=a3x2+b3x
则
∴a3=-
b3=3
∴抛物线的解析式是y=-
x2+3x
∴顶点坐标是(3,
)(10分).
∵
| 1 |
| 2 |
∵XA>0,YA>0
∴xAyA=8
设y=
| k |
| x |
∴xAyA=k
∴k=8.
∴设比例函数解析式为y=
| 8 |
| x |
②∵yA=4,
∴xA=2
∴A(2,4)
∴OB=2,AB=4
当∠AP1B=∠AOB时,△AOB≌△APB
∴PB=OB=2,∴P1(4,0)(3分)
当∠AP2B=∠OAB时△AOB∽△P2AB
可以由
| AB |
| BP2 |
| OB |
| AB |
| 4 |
| BP2 |
| 2 |
| 4 |
当P3在x轴负半轴上时,
且P3与P2关于点B对称也满足△AOB∽△P3BA
由P2(10,0),B(2,0),
∴P3(-6,0).(5分)
③当抛物线经过P1(4,0),O(0,0),A(2,4)时
设解析式为y=ax2+bx+c
解
|
|
∴解析式为y=-x2+4x
∴顶点坐标是(2,4)(6分)
当抛物线经过P2(10,0),O(0,0),A(2,4)时
设所求抛物线为y=a2x2+b2x
则
|
|
∴y=-
| 1 |
| 4 |
| 5 |
| 2 |
| 1 |
| 4 |
| 25 |
| 4 |
∴顶点坐标是(5,
| 25 |
| 4 |
设经过P3(-6,0),O(0,0),A(2,4)的解析式为:y=a3x2+b3x
则
|
| 1 |
| 2 |
∴抛物线的解析式是y=-
| 1 |
| 2 |
∴顶点坐标是(3,
| 9 |
| 2 |
点评:此题难度中等,考查反比例、二次函数的图象性质及用待定系数法求函数的解析式,以及两三角形相似等知识点.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
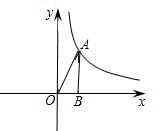 如图,第一象限内的点A在某反比例函数的图象上,过A作AB⊥x轴,垂足为B,连接AO,已知△AOB的面积为4.
如图,第一象限内的点A在某反比例函数的图象上,过A作AB⊥x轴,垂足为B,连接AO,已知△AOB的面积为4.
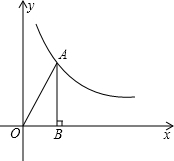 已知△AOB的面积为4.
已知△AOB的面积为4.