题目内容
1.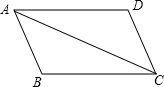 已知:如图四边形ABCD中,AB=CD,AD=BC.
已知:如图四边形ABCD中,AB=CD,AD=BC.(1)请说明△ABC≌△CDA的理由;
(2)线段AB与CD平行吗?AD与BC呢?为什么?
分析 (1)根据SSS容易证明△ABC≌△CDA;
(2)先由平行四边形的判定方法证明四边形ABCD是平行四边形,再由平行四边形的性质即可得出结论.
解答 解:(1)理由:
在△ABC与△CDA中,
$\left\{\begin{array}{l}{AB=CD}&{\;}\\{BC=DA}&{\;}\\{AC=CA}&{\;}\end{array}\right.$,
∴△ABC≌△CDA(SSS);
(2)AB∥CD,AD∥BC;理由如下:
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
点评 本题考查了全等三角形的判定方法以及平行四边形的判定与性质;熟练掌握全等三角形的判定方法和平行四边形的判定与性质是解题的关键.

练习册系列答案
相关题目
11.若四边形的对角线互相垂直且相等,则它一定是( )
| A. | 菱形 | B. | 正方形 | ||
| C. | 等腰梯形 | D. | 以上说法均不正确 |
12. 如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )
如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )
 如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )
如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )| A. | 115° | B. | 105° | C. | 95° | D. | 85° |
11.要使代数式$\frac{\sqrt{x+3}}{x-1}$有意义,则x应满足( )
| A. | x≠1 | B. | x>-3且x≠1 | C. | x≥-3 | D. | x≥-3且x≠1 |
