��Ŀ����
����Ŀ����ͼ��������![]() ��
��![]() ��b�dz�������
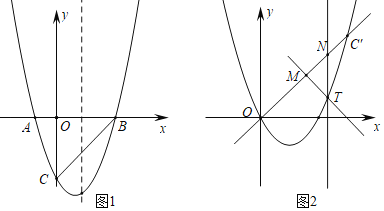
��b�dz�������![]() ��0����x�ύ��A��B���㣬��y�ύ�ڵ�C������A��B���������ֱ���A(��1��0)��B(3��0)
��0����x�ύ��A��B���㣬��y�ύ�ڵ�C������A��B���������ֱ���A(��1��0)��B(3��0)
��1�����������ߵĽ���ʽ���ڶ���D������Ϊ_______����ֱ��BD�Ľ���ʽΪ______��
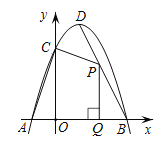
��2����PΪ�߶�BD�ϵ�һ�����㣬�������Ϊm������P��PQ��x���ڵ�Q����mΪ��ֵʱ���ı���PQOC��������
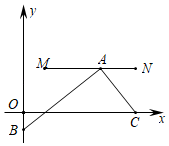
��3������M���������ڵ�һ�����ϵ�һ�����㣬����M��MN��AC��![]() ���ڵ�N������M������Ϊ_______ʱ���ı���MNAC��ƽ���ı��Σ�
���ڵ�N������M������Ϊ_______ʱ���ı���MNAC��ƽ���ı��Σ�
���𰸡���1����![]() ����(1��4)����
����(1��4)����![]() ����2����
����2����![]() ʱ��S���ֵ=
ʱ��S���ֵ=![]() ����3��(2��3)
����3��(2��3)
��������
��1���ٰѵ�A����B���������![]() �����
�����![]() ��b���ɣ��ڸ��ݶ������깫ʽ
��b���ɣ��ڸ��ݶ������깫ʽ![]() ��⣻����ֱ��BD�Ľ���ʽΪ
��⣻����ֱ��BD�Ľ���ʽΪ![]() ������B����D��������뼴�ɣ�
������B����D��������뼴�ɣ�
��2�������C���꣬����ֱ�����ε������ʽ�ɵ��ı���PQOC�����s��m�Ĺ�ϵʽ���������������ֵ��
��3��Ҫʹ�ı���MNAC��ƽ���ı���ֻҪ![]() ���ɣ����Ե�M���C����������ͬ���ɴ˿���õ�M����.
���ɣ����Ե�M���C����������ͬ���ɴ˿���õ�M����.
�⣺��1���ٰ�A����1��0����B��3��0������![]() ����
����
![]()
���![]()
��![]()
�ڵ�![]() ʱ��
ʱ��![]()
���Զ�������Ϊ��1��4��
����ֱ��BD�Ľ���ʽΪ![]() ������B��3��0������D��1��4������������
������B��3��0������D��1��4������������
![]() �����
�����![]()
����ֱ��BD�Ľ���ʽΪ![]()
��2���ߵ�P�ĺ�����Ϊm�����P��������Ϊ![]() ��
��
��![]() ʱ��
ʱ��
![]()
��C��0��3����
�������֪��
OC=3��OQ=m��PQ=![]() ��
��
��s=![]()
=![]()
=![]() .
.
�ߣ�1��0��1��![]() ��3��
��3��
�൱![]() ʱ��s���ֵ=
ʱ��s���ֵ=![]()
��ͼ��MN��AC��Ҫʹ�ı���MNAC��ƽ���ı���ֻҪ![]() ����.
����.

���M������Ϊ![]() ��
��
��![]() ��֪��
��֪��![]()
![]()
![]()
���![]() ��0���������⣬��ȥ��
��0���������⣬��ȥ��
![]()
����M������Ϊ��2��3��ʱ���ı���MNAC��ƽ���ı��Σ�