Question

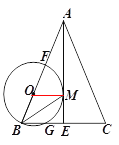
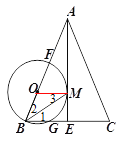
【题目】如图，在△ABC中,AB=AC,AE是BC边上的高线，BM平分∠ABC交AE于点M，经过B，M 两点的⊙O交BC于点G，交AB于点F ，FB为⊙O的直径．

（1）求证：AM是⊙O的切线

（2）当BE=3，cosC=时，求⊙O的半径．

Answer 1

【答案】(1)见解析；(2)

【解析】分析：(1)连结 根据BM平分∠ABC，得到根据，得到根据等量代换得到证明OM∥BC，AE是BC边上的高线，得到，即可证明.

根据cosC==,求出的长度，根据, cos∠AOM = cosC=,

得到AO=, AB=+OB=,求解即可.

详解：(1)连结

∵BM平分∠ABC，

∴ 又

∴

∴ OM∥BC，

AE是BC边上的高线

∴

∴

∴AM是⊙O的切线

（2）∵,

∴,

∴E是BC中点,∴,

∵cosC==,

∴

∵OM∥ BC，,

∴, ∴

又

∴

在中，cos∠AOM = cosC=,

∴AO=,

AB=+OB=,

而

∴=,

OM=,

∴⊙O的半径是.