题目内容
【题目】[阅读理解]射线![]() 是
是![]() 内部的一条射线,若
内部的一条射线,若![]() 则我们称射线
则我们称射线![]() 是射线
是射线![]() 的伴随线.
的伴随线.
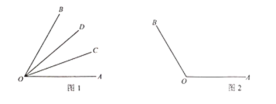
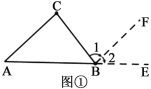
例如,如图1,![]() ,则
,则![]() ,称射线
,称射线![]() 是射线
是射线![]() 的伴随线:同时,由于
的伴随线:同时,由于![]() ,称射线
,称射线![]() 是射线
是射线![]() 的伴随线.
的伴随线.
[知识运用]
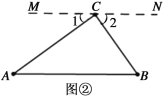
(1)如图2,![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,则
的伴随线,则![]() ,若
,若![]() 的度数是
的度数是![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,射线
的伴随线,射线![]() 是
是![]() 的平分线,则
的平分线,则![]() 的度数是 .(用含
的度数是 .(用含![]() 的代数式表示)
的代数式表示)
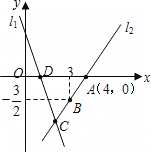
(2)如图,如![]() ,射线
,射线![]() 与射线
与射线![]() 重合,并绕点
重合,并绕点![]() 以每秒
以每秒![]() 的速度逆时针旋转,射线
的速度逆时针旋转,射线![]() 与射线
与射线![]() 重合,并绕点
重合,并绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,当射线
的速度顺时针旋转,当射线![]() 与射线
与射线![]() 重合时,运动停止,现在两射线同时开始旋转.
重合时,运动停止,现在两射线同时开始旋转.

①是否存在某个时刻![]() (秒),使得
(秒),使得![]() 的度数是
的度数是![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
②当![]() 为多少秒时,射线
为多少秒时,射线![]() 中恰好有一条射线是其余两条射线的伴随线.
中恰好有一条射线是其余两条射线的伴随线.
【答案】(1)![]() ,
,![]() ;(2)①存在,当
;(2)①存在,当![]() 秒或25秒时,∠COD的度数是20
秒或25秒时,∠COD的度数是20![]() ;②当
;②当![]() ,
,![]() ,
,![]() ,
,![]() 时,OC、OD、OA中恰好有一条射线是其余两条射线的伴随线.
时,OC、OD、OA中恰好有一条射线是其余两条射线的伴随线.
【解析】
(1)根据伴随线定义即可求解;
(2)①利用分类讨论思想,分相遇之前和之后进行列式计算即可;
②利用分类讨论思想,分相遇之前和之后四个图形进行计算即可.
(1)∵![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,
的伴随线,
根据题意,![]() ,则
,则![]() ;
;
∵![]() 的度数是
的度数是![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,射线
的伴随线,射线![]() 是
是![]() 的平分线,
的平分线,
∴![]() ,
,![]() ,
,
∴![]() ;
;
故答案为:![]() ,
,![]() ;
;
(2)射线OD与OA重合时,![]() (秒),
(秒),
①当∠COD的度数是20°时,有两种可能:
若在相遇之前,则![]() ,
,
∴![]() ;
;
若在相遇之后,则![]() ,
,
∴![]() ;
;
所以,综上所述,当![]() 秒或25秒时,∠COD的度数是20°;
秒或25秒时,∠COD的度数是20°;
②相遇之前:
(i)如图1,

OC是OA的伴随线时,则![]() ,
,
即![]() ,
,
∴![]() ;
;
(ii)如图2,
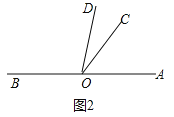
OC是OD的伴随线时,
则![]() ,
,
即![]() ,
,
∴![]() ;
;
相遇之后:
(iii)如图3,
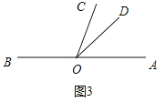
OD是OC的伴随线时,
则![]() ,
,
即![]() ,
,
∴![]() ;
;
(iv)如图4,

OD是OA的伴随线时,则![]() ,
,
即![]() ,
,
∴![]() ;
;
所以,综上所述,当![]() ,
,![]() ,
,![]() ,
,![]() 时,OC、OD、OA中恰好有一条射线是其余两条射线的伴随线.
时,OC、OD、OA中恰好有一条射线是其余两条射线的伴随线.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案