题目内容
若抛物线y=-x2+2ax+b的顶点在直线mx-y-2m+1=0上移动,且与抛物线y=x2有公共点,求m的取值范围.
解:∵y=-x2+2ax+b=-(x-a)2+a2+b,
∴顶点坐标为(a,a2+b),
代入mx-y-2m+1=0中,得ma-(a2+b)-2m+1=0,
即b=ma-a2-2m+1,
联立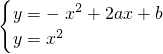 ,
,
解得-2x2+2ax+b=0,
∵两抛物线有公共点,
∴△=(2a)2-4×(-2)×b≥0,
即a2+2b≥0,
a2+2(ma-a2-2m+1)≥0,
整理,得2(a-2)m≥a2-2,
当a=2时,无解,
当a>2时,
m≥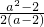 =
= [a-2+
[a-2+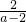 +4]≥
+4]≥ +2,当a=2+
+2,当a=2+ 时取等号;
时取等号;
当a<2时,
m≤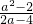 =
= [a-2+
[a-2+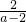 +4]≤-
+4]≤- +2,当a=2-
+2,当a=2- 时取等号.
时取等号.
分析:用配方法将抛物线y=-x2+2ax+b写成顶点式,求出顶点坐标,代入直线mx-y-2m+1=0中,再联立两条抛物线的解析式,当两抛物线有交点时,△≥0,解不等式即可.
点评:本题考查了抛物线的顶点坐标的求法,两抛物线的交点坐标的求法,以及解不等式的相关知识,分类讨论问题.
∴顶点坐标为(a,a2+b),
代入mx-y-2m+1=0中,得ma-(a2+b)-2m+1=0,
即b=ma-a2-2m+1,
联立
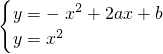 ,
,解得-2x2+2ax+b=0,
∵两抛物线有公共点,
∴△=(2a)2-4×(-2)×b≥0,
即a2+2b≥0,
a2+2(ma-a2-2m+1)≥0,
整理,得2(a-2)m≥a2-2,
当a=2时,无解,
当a>2时,
m≥
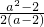 =
= [a-2+
[a-2+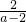 +4]≥
+4]≥ +2,当a=2+
+2,当a=2+ 时取等号;
时取等号;当a<2时,
m≤
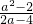 =
= [a-2+
[a-2+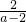 +4]≤-
+4]≤- +2,当a=2-
+2,当a=2- 时取等号.
时取等号.分析:用配方法将抛物线y=-x2+2ax+b写成顶点式,求出顶点坐标,代入直线mx-y-2m+1=0中,再联立两条抛物线的解析式,当两抛物线有交点时,△≥0,解不等式即可.
点评:本题考查了抛物线的顶点坐标的求法,两抛物线的交点坐标的求法,以及解不等式的相关知识,分类讨论问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若抛物线y=x2-
x-1与x轴有交点,则k的取值范围是( )
| k-1 |
| A、k>-3 | B、k≥-3 |
| C、k≥1 | D、-3≤k≤1 |