题目内容
已知等腰Rt△ABC斜边上一点P，求证：AP2+BP2=2CP2．
考点：勾股定理,等腰直角三角形
专题：证明题
分析：作出图形，过点C作CD⊥AB于D，根据等腰直角三角形的性质可得AD=BD=CD，设为a，设PD=x，用a、x表示出AP、BP，然后求出AP2+BP2，再利用勾股定理表示出CP2，整理即可得证．
解答：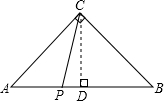
证明：如图，过点C作CD⊥AB于D，
∵△ABC是等腰直角三角形，
∴AD=BD=CD，设为a，
设PD=x，则AP=a-x，BP=a+x，
所以，AP2+BP2=（a-x）2+（a+x）2=2a2+2x2，
在Rt△CDP中，CP2=CD2+PD2=a2+x2，
∵2a2+2x2=2（a2+x2），
∴AP2+BP2=2CP2．
证明：如图，过点C作CD⊥AB于D，∵△ABC是等腰直角三角形，
∴AD=BD=CD，设为a，
设PD=x，则AP=a-x，BP=a+x，
所以，AP2+BP2=（a-x）2+（a+x）2=2a2+2x2，
在Rt△CDP中，CP2=CD2+PD2=a2+x2，
∵2a2+2x2=2（a2+x2），
∴AP2+BP2=2CP2．
点评：本题考查了勾股定理，等腰直角三角形的性质，作辅助线构造出以CP为斜边的直角三角形是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
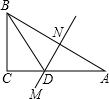如图，在△ABC中，∠C=90°，AC=24cm，AB的垂直平分线MN交AC于D，连接BD，若cos∠BDC=| 3 |
| 5 |
| A、12cm | B、9cm |
| C、24cm | D、14cm |
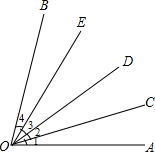如图，∠1=∠2=∠3=∠4，根据图形回答：
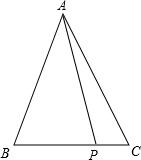在△ABC中，AB=AC=5cm，P是BC边上一点，证明：无论底边BC的长度是多少，以及点P在BC上的位置如何，PA2+PB•PC的值总是常数．
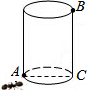如图，圆柱体蜜桶的半径为1cm，高为3cm，桶内所装蜜的高度距点B为1cm，在点A处有一只蚂蚁，若蚂蚁沿圆柱体的外表面爬行到内表面BC 线的某点处吃蜜，它爬行的最短路线是多少？