题目内容
已知方程x2+2ax-2b+1=0的两个根与-x2+（a-3）x+b2-1=0的两个根分别相等，求a、b的值．
考点：一元二次方程的解
专题：
分析：由于方程x2+2ax-2b+1=0的两个根与-x2+（a-3）x+b2-1=0的两个根分别相等，所以
=
=
，由此求出a、b的值．
| 1 |
| -1 |
| 2a |
| a-3 |
| -2b+1 |
| b2-1 |
解答：解：∵方程x2+2ax-2b+1=0的两个根与-x2+（a-3）x+b2-1=0的两个根分别相等，
∴
=
=
，
∴a=1，b=0或2．
∴
| 1 |
| -1 |
| 2a |
| a-3 |
| -2b+1 |
| b2-1 |
∴a=1，b=0或2．
点评：本题考查了一元二次方程的解（根）的意义：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．又因为只含有一个未知数的方程的解也叫做这个方程的根，所以，一元二次方程的解也称为一元二次方程的根．
练习册系列答案
相关题目
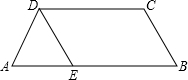如图，已知DC∥AB，∠C=∠DEB，求证：DE∥BC．