题目内容
3．
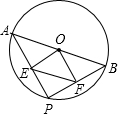如图，AB是⊙O的直径，点P是⊙O上的动点（P与A，B不重合），连结AP，PB，过点O分别作OE⊥AP于E，OF⊥BP于F．若AB=12，当点P在⊙O上运动时，线段EF的长会不会改变．若会改变，请说明理由；若不会改变，请求出EF的长．
分析 由于OE、OF都经过圆心，且垂直于AP、BP，由垂径定理知E、F分别是AP、PB的中点，即EF是△APB的中位线，由此可得到EF=$\frac{1}{2}$AB=6，因此EF的长不会改变．
解答 解：EF的长不会改变．EF=6．
∵OE⊥AP于E，OF⊥BP于F，
∴AE=EP，BF=FP，
∴EF=$\frac{1}{2}$AB=6．
点评 此题考查了垂径定理、圆周角定理、三角形中位线定理等知识，综合性比较强．
练习册系列答案
相关题目
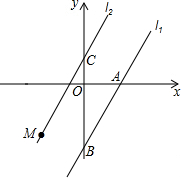如图，一次函数l1：y=2x+b的图象与x轴、y轴分别相交于A、B两点，A的坐标为（2，0），y轴正半轴上有一点C（0，$\frac{3}{2}$），过点C有一条直线l2∥l1（l2与l1的k相等，即k2=k1），M是l2上任意一点．
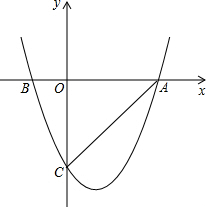如图，抛物线y=x2-2x-3交x轴于A、B，交y轴于C；