题目内容
12．直角三角形两锐角的平分线相交所夹的钝角为（ ）| A． | 125° | B． | 135° | C． | 145° | D． | 150° |
分析 作出图形，根据直角三角形两锐角互余可得∠BAC+∠ABC=90°，再根据角平分线的定义可得∠OAB+∠OBA=45°，然后根据三角形的内角和定理列式计算即可得解．
解答 解：如图，∵∠C=90°，
∴∠BAC+∠ABC=180°-90°=90°，
∵AD、BE分别是∠BAC和∠ABC的平分线，
∴∠OAB+∠OBA=$\frac{1}{2}$×90°=45°，
∴∠AOB=180°-（∠OAB+∠OBA）=180°-45°=135°．
故选B．
点评 本题考查了直角三角形两锐角互余的性质，角平分线的定义，三角形内角和定理，整体思想的利用是解题的关键，作出图形更形象直观．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售，已知每天包装大黄米的质量是包装江米质量的$\frac{5}{4}$倍，且每天包装大黄米和江米的质量之和为45千克．
20．如果点A（m+1，1-2m）在第四象限，那么m的取值范围是（ ）
| A． | m＞-1 | B． | m＞$\frac{1}{2}$ | C． | -1＜m＜$\frac{1}{2}$ | D． | 0＜m＜$\frac{1}{2}$ |
17．若a＞b，则下列不等式一定成立的是（ ）
| A． | $\frac{b}{a}$＜1 | B． | $\frac{b}{a}$＞1 | C． | -a＞-b | D． | b-a＜0 |
4．
如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x≥ax+4的解集为（ ）
如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x≥ax+4的解集为（ ）| A． | x≤3 | B． | x≥3 | C． | x≤$\frac{3}{2}$ | D． | x≥$\frac{3}{2}$ |
1．已知二元一次方程2x-y=1，用y的代数式表示x为（ ）
| A． | x=$\frac{1+y}{2}$ | B． | x=$\frac{1-y}{2}$ | C． | y=1-2x | D． | y=2x-1 |
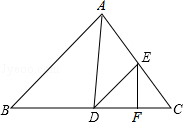如图，在△ABC中，∠B=54°，AD平分∠CAB，交BC于D，E为AC边上一点，连结DE，∠EAD=∠EDA，EF⊥BC于点F．求∠FED的度数．