题目内容
 如图,点D、E在AB上,点F在AC上,点G在BC上,四边形DEFG是正方形,且DE2=BD•AE,△ABC是直角三角形吗?为什么?
如图,点D、E在AB上,点F在AC上,点G在BC上,四边形DEFG是正方形,且DE2=BD•AE,△ABC是直角三角形吗?为什么?
解:△ABC是直角三角形.理由如下:
∵四边形DEFG是正方形,
∴DE=GD=EF,
∵DE2=BD•AE,
∴ =
=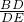 ,
,
即 =
= ,
,
又∵∠BDG=∠FEA=90°,
∴△AEF∽△GDB,
∴∠A=∠BGD,
在Rt△BGD中,∠B+∠BGD=180°-90°=90°,
∴∠A+∠B=90°,
∴∠C=180°-(∠A+∠B)=180°-90°=90°,
∴△ABC是直角三角形.
分析:根据正方形的四条边都相等可得DE=GD=EF,然后把乘积式DE2=BD•AE转化为比例式,从而证明△AEF与△GDB相似,根据相似三角形的对应角相等得到∠A=∠BGD,再利用角的关系推出∠A+∠B=90°,所以△ABC是直角三角形.
点评:本题考查了相似三角形的判定与性质,正方形的四条边都相等的性质,把乘积式转化为比例式,从而证明两三角形相似是解题的关键,也是本题的突破口.
∵四边形DEFG是正方形,
∴DE=GD=EF,
∵DE2=BD•AE,
∴
 =
=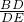 ,
,即
 =
= ,
,又∵∠BDG=∠FEA=90°,
∴△AEF∽△GDB,
∴∠A=∠BGD,
在Rt△BGD中,∠B+∠BGD=180°-90°=90°,
∴∠A+∠B=90°,
∴∠C=180°-(∠A+∠B)=180°-90°=90°,
∴△ABC是直角三角形.
分析:根据正方形的四条边都相等可得DE=GD=EF,然后把乘积式DE2=BD•AE转化为比例式,从而证明△AEF与△GDB相似,根据相似三角形的对应角相等得到∠A=∠BGD,再利用角的关系推出∠A+∠B=90°,所以△ABC是直角三角形.
点评:本题考查了相似三角形的判定与性质,正方形的四条边都相等的性质,把乘积式转化为比例式,从而证明两三角形相似是解题的关键,也是本题的突破口.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 如图,点D,E分别在AB,AC上,且AD=AE,∠BDC=∠CEB.
如图,点D,E分别在AB,AC上,且AD=AE,∠BDC=∠CEB.
 (2012•朝阳区二模)已知:如图,点D、E分别在AB、AC上,BE与CD相交于点F,BD=CE,∠B=∠C.
(2012•朝阳区二模)已知:如图,点D、E分别在AB、AC上,BE与CD相交于点F,BD=CE,∠B=∠C.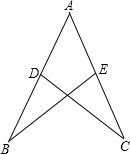 如图,点D,E分别在AB/AC上,
如图,点D,E分别在AB/AC上, 如图,点D、E分别在AB、AC上,AD=AE,∠B=∠C,CD与BE交于点O.
如图,点D、E分别在AB、AC上,AD=AE,∠B=∠C,CD与BE交于点O.