题目内容
17．
如图，三角形ABC是直角三角形，BO是它斜边AC上的中线，延长BO至D，使OD=OB，连接AD，DC，求证：四边形ABCD是矩形．
分析 首先利用对角线互相平分证得四边形ABCD是平行四边形，然后利用对角线相等证得为矩形．
解答 解：∵Rt△ABC中，CO为斜边的中线，
∴AO=CO=BO，
∵CO=OD，
∴AO=CO=BO=DO，
∴四边形ABCD为平行四边形，
∵AC=DB，
∴四边形ABCD为矩形．
点评 本题考查了矩形的判定及直角三角形的性质，解题的关键是了解有关矩形的判定定理，难度不大．
练习册系列答案
相关题目
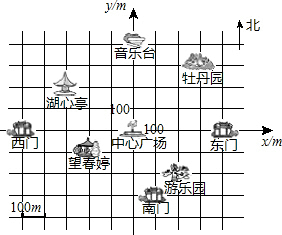如图，这是人民公园的景区示意图．以中心广场为原点，分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系，规定一个单位长度代表100m长．已知各建筑物都在坐标平面网格的格点上，且东门的坐标为（400，0）．
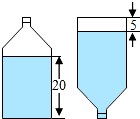有种饮料瓶如图，它的直径是4cm，里面的水高度是20cm，把瓶盖拧紧倒置放平，无水部分圆柱高度是5cm，求饮料瓶的容积是多少？（结果保留整数）
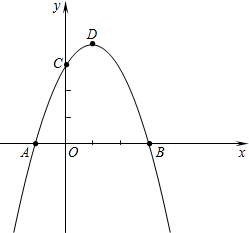如图，在平面直角坐标系中，二次函数y=ax2+bx+c（a≠0）的图象经过点A（-1，0）、点B（3，0）、点C（0，3）．
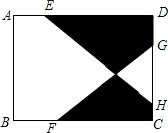如图，在矩形ABCD中，点E、F分别在边AD、BC上，点G、H在DC边上，且AE：AD=1：4，BF：BC=1：4，GH=$\frac{1}{2}$DC，AB=10，BC=12，则图中阴影部分面积为52.5．