题目内容
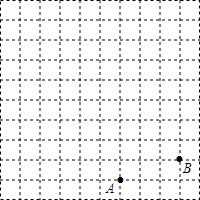
如图,在正方形网格中,每个小正方形的边长都为1,点A,点B在网格中的位置如图所示.
(1)建立适当的平面直角坐标系,使点A,点B的坐标分别为(1,﹣4)(4,﹣3);
(2)点C的坐标为(2,﹣2),在平面直角坐标系中标出点C的位置,连接AB,BC,CA,则△ABC是__________三角形;
(3)在图中作出△ABC关于x轴对称的图形△A1B1C1.
【考点】作图-轴对称变换.
【分析】(1)根据题意建立适当的坐标系即可;
(2)根据勾股定理的逆定理判断出△ABC的形状即可;
(3)作出各点关于x轴的对称点,再顺次 连接即可.
连接即可.
【解答】解:(1)如图所示;
(2)∵AC2=BC2=12+22=5,AB2=32+12=10,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
故答案为:直角;
(3)如图所示.

【点评】本题考查的是作图﹣轴对称变换,熟知关于x轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
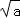 ,我们把
,我们把 =0,求a+b的立方根.
=0,求a+b的立方根.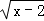 +
+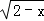 +2,求xy的平方根.
+2,求xy的平方根.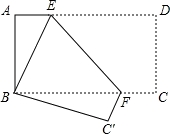
 的平方根为__________.
的平方根为__________.
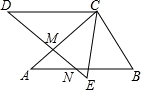
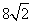 ;
;