Question

【题目】张老师将“校园诗词大赛”所有参赛选手的比赛成绩(得分均为整数)进行整理，并分别绘制成扇形统计图和频数直方图，部分信息如下：

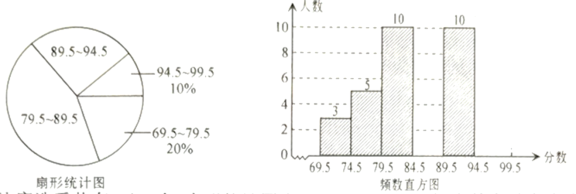
（1）本次比赛选手共有_ 人，扇形统计图中“”这一组人数占总参赛人数的百分比为_ ，频数直方图中“”这一组的人数为__ ；

（2）赛前规定，成绩由高到低前的参赛选手获奖某参赛选手的比赛成绩为分，试判断他能否获奖，并说明理由；

（3）成绩前四名是名男生和名女生，若从他们中任选人作为全区“诗词大会”重点培训对象，试求恰好选中男女的概率．

Answer 1

【答案】（1）40，45%，4；（2）能获奖，理由见解析；（3）．

【解析】

（1）根据扇形统计图和频数分布直方图得出69.5~79.5这组所占的百分比和频数，可得本次比赛选手总人数；计算89.5~94.5这组所占百分比，用总数乘以79.5~89.5这组所占的百分比即可得到结果；用总数乘以94.5~99.5这组所占的百分比即可得到结果；

（2）计算出前55%的人数其最低分值，可以判断结果；

（3）画树状图得到所有可能的情况，再找出符合条件的情况后，用概率公式进行求解即可．

（1）由扇形统计图可知69.5~79.5这组所占为20%，

由频数分布直方图得69.5~79.5这组的频数为：3+5=8，

∴参赛选手总数为：（人）

又∵89.5~94.5这组所占的百分比为：10

∴79.5~89.5这组所占的百分比为：

∴94.5~99.5这组的频数为：40（人）

他能获奖．理由如下：“”这一组人数为分以上的人数占总参赛人数的百分比为，即分以上的选手可获奖

画树状图如解图：

由树状图知，共有种等可能结果，

其中恰好选中男女的结果共有种，

故．