题目内容
17. 如图,抛物线y=ax2+2x经过点A(4,0).将这条抛物向左平移后与原抛物线交与点C,点C在x轴的上方,此时点A移动到点B的位置.当△OBC为等边三角形时,边OB的长是( )
如图,抛物线y=ax2+2x经过点A(4,0).将这条抛物向左平移后与原抛物线交与点C,点C在x轴的上方,此时点A移动到点B的位置.当△OBC为等边三角形时,边OB的长是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 4-2$\sqrt{3}$ | D. | 8-4$\sqrt{3}$ |
分析 先求得抛物线的解析式,然后设OB=m,根据等边三角形的性质得出C的坐标,代入解析式即可求得m的值,从而求得OB的长.
解答 解:∵抛物线y=ax2+2x经过点A(4,0).
∴16a+8=0,
解得a=-$\frac{1}{2}$,
∴抛物线为y=-$\frac{1}{2}$x2+2x,
设OB=m,
∵△OBC为等边三角形,
∴C($\frac{1}{2}$m,$\frac{\sqrt{3}}{2}$m),
代入y=-$\frac{1}{2}$x2+2x得$\frac{\sqrt{3}}{2}$m=-$\frac{1}{8}$m2+m,
解得m=8-4$\sqrt{3}$,
∴OB=8-4$\sqrt{3}$;
故选D.
点评 本题考查了二次函数的图象与几何变换,求得C的坐标是解题的关键.

练习册系列答案
相关题目
7. 如图,在平行四边形ABCD中,AC、BD相交于点O,则下列结论不一定成立的是( )
如图,在平行四边形ABCD中,AC、BD相交于点O,则下列结论不一定成立的是( )
 如图,在平行四边形ABCD中,AC、BD相交于点O,则下列结论不一定成立的是( )
如图,在平行四边形ABCD中,AC、BD相交于点O,则下列结论不一定成立的是( )| A. | BO=DO | B. | S△COD=S△AOD | C. | ∠BAD=∠BCD | D. | AC=BD |
8.下列四个数中,最小的数是( )
| A. | 0 | B. | -$\frac{1}{2}$ | C. | -2 | D. | $\sqrt{2}$ |
2.统计显示,2015年汕头市中考学生人数和高考学生人数合计大约是13.3万人,将13.3万用科学记数法表示应为( )
| A. | 13.3×102 | B. | 1.33×103 | C. | 1.33×104 | D. | 1.33×105 |
9.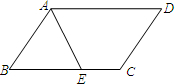 如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )
如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )
 如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )
如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
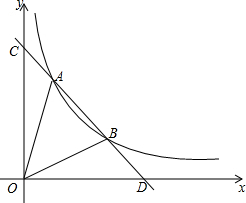 如图,一次函数的图形与y轴、x轴交于C、D两点,与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A、B两点,且AB=2BD,则△AOB的面积为8.
如图,一次函数的图形与y轴、x轴交于C、D两点,与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A、B两点,且AB=2BD,则△AOB的面积为8.