题目内容
已知
；
；
；
…
（1）猜想填空：
______2______2
（2）计算：①13+23+33+…+993+1003；②23+43+63+…+983+1003．
解：（1）13+23+33+…+n3=
n2（n+1）2；
（2）①13+23+33+…+993+1003=×1002×1012，
②23+43+63+…+983+1003
=23•（13+23+33+…+493+503）
=8××502×512
=13005000．
故答案为：n；（n+1）．
分析：（1）观察不难发现，从1开始的连续自然数的立方和等于最后一个数的平方与比它大1的数的平方的积的，然后写出即可；
（2）①根据（1）的公式列式计算即可得解；
②先提取23，再利用（1）的公式列式计算即可得解．
点评：本题是对数字变化规律的考查，观察出等式右边平方的两个数的底数与左边最后一个数的关系是解题的关键．
n2（n+1）2；（2）①13+23+33+…+993+1003=
×1002×1012，②23+43+63+…+983+1003
=23•（13+23+33+…+493+503）
=8×
×502×512=13005000．
故答案为：n；（n+1）．
分析：（1）观察不难发现，从1开始的连续自然数的立方和等于最后一个数的平方与比它大1的数的平方的积的
，然后写出即可；（2）①根据（1）的公式列式计算即可得解；
②先提取23，再利用（1）的公式列式计算即可得解．
点评：本题是对数字变化规律的考查，观察出等式右边平方的两个数的底数与左边最后一个数的关系是解题的关键．
练习册系列答案
相关题目
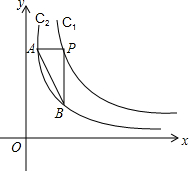如图：已知反比例C1：