题目内容
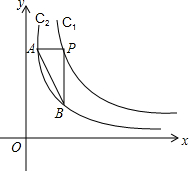 如图:已知反比例C1:y=
如图:已知反比例C1:y=| k1 |
| x |
| k2 |
| x |
(1)当取k1=4,k2=1,
①点P坐标为(2,2)时,则S三角形ABP=
| 9 |
| 8 |
| 9 |
| 8 |
②点P坐标为(1,4)时,S三角形ABP=
| 9 |
| 8 |
| 9 |
| 8 |
(2)通过观察、思考(1)的计算结果,你能猜想到△ABP的面积有何规律或特征?并请你用含k1、k2的代数式表示△ABP的面积.
分析:(1)根据AP∥x轴,BP∥y轴,得到AP⊥PB,从而知道,点B、点P横坐标相同,点A、点P纵坐标相同,求出A点横坐标xA,B点纵坐标yB,再利用P点坐标,求出AP、BP的长,从而得到三角形的面积.
(2)根据AP∥x轴,BP∥y轴,得到AP⊥PB,从而知道,点B、点P横坐标相同,点A、点P纵坐标相同,设点P的横坐标为a,则纵坐标为
,代入解析式求出A(
,
),B(a,
),从而求出AP和BP的长,表示出S三角形ABP.
(2)根据AP∥x轴,BP∥y轴,得到AP⊥PB,从而知道,点B、点P横坐标相同,点A、点P纵坐标相同,设点P的横坐标为a,则纵坐标为
| k1 |
| a |
| ak2 |
| k1 |
| k1 |
| a |
| k2 |
| a |
解答:解:(1)当取k1=4,k2=1时,反比例C1:y=
;C2:y=
可化为C1:y=
,C2:y=
;
∵AP∥x轴,BP∥y轴,
∴AP⊥PB,
∴点B、点P横坐标相同,点A、点P纵坐标相同,
①点P坐标为(2,2)时,设A点坐标为(xA,2),B点坐标为(2,yB),
把A点坐标(xA,2)代入y=
得,xA=
;
把B点坐标(2,yB)代入y=
得,yB=
,
∴S三角形ABP=
×AP×BP
=
×(2-
)×(2-
)
=
,
②点P坐标为(1,4)时,设A点坐标为(xA,4),B点坐标为(1,yB),
把A点坐标(xA,4)代入y=
得,xA=
;
把B点坐标(1,yB)代入y=
得,yB=1,
∴S三角形ABP=
×AP×BP
=
×(1-
)×(4-1)
=
.
故答案为案为
,
.
(2)不论点P在双曲线C1上的任意处,△ABP的面积等于一个定值.
∵PA∥x轴,PB∥y轴,
∴∠APB=90°,
设点P的横坐标为a,则纵坐标为
,
又∵A与P的纵坐标相同,
∴
=
,x=
,
∴A(
,
),
∵B与P的横坐标相同,
∴y=
,
∴B(a,
).
AP=a-
=
=a×
,PB=
-
=
.
∴S三角形ABP=
×a×
×
=
.
| k1 |
| x |
| k2 |
| x |
| 4 |
| x |
| 1 |
| x |
∵AP∥x轴,BP∥y轴,
∴AP⊥PB,
∴点B、点P横坐标相同,点A、点P纵坐标相同,
①点P坐标为(2,2)时,设A点坐标为(xA,2),B点坐标为(2,yB),
把A点坐标(xA,2)代入y=
| 1 |
| x |
| 1 |
| 2 |
把B点坐标(2,yB)代入y=
| 1 |
| x |
| 1 |
| 2 |
∴S三角形ABP=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 9 |
| 8 |
②点P坐标为(1,4)时,设A点坐标为(xA,4),B点坐标为(1,yB),
把A点坐标(xA,4)代入y=
| 1 |
| x |
| 1 |
| 4 |
把B点坐标(1,yB)代入y=
| 1 |
| x |
∴S三角形ABP=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 4 |
=
| 9 |
| 8 |
故答案为案为
| 9 |
| 8 |
| 9 |
| 8 |
(2)不论点P在双曲线C1上的任意处,△ABP的面积等于一个定值.
∵PA∥x轴,PB∥y轴,
∴∠APB=90°,
设点P的横坐标为a,则纵坐标为
| k1 |
| a |
又∵A与P的纵坐标相同,
∴
| k1 |
| a |
| k2 |
| x |
| ak2 |
| k1 |
∴A(
| ak2 |
| k1 |
| k1 |
| a |
∵B与P的横坐标相同,
∴y=
| k2 |
| a |
∴B(a,
| k2 |
| a |
AP=a-
| ak2 |
| k1 |
| ak1-ak2 |
| k1 |
| k1-k2 |
| k1 |
| k1 |
| a |
| k2 |
| a |
| k1-k2 |
| a |
∴S三角形ABP=
| 1 |
| 2 |
| k1-k2 |
| k1 |
| k1-k2 |
| a |
| (k1-k2)2 |
| 2k1 |
点评:本题考查了反比例函数综合题,涉及函数图象上点的坐标特征、三角形的面积与坐标的关系,是一道好题.

练习册系列答案
相关题目




 如图:已知反比例C1:
如图:已知反比例C1: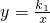 ;C2:
;C2: ,且k1>k2>0,点P是双曲线C1上的一点,过P点引x、y轴的平行线交双曲线C2于A、B两点,连接AB.
,且k1>k2>0,点P是双曲线C1上的一点,过P点引x、y轴的平行线交双曲线C2于A、B两点,连接AB.
 ;C2:
;C2: ,且k1>k2>0,点P是双曲线C1上的一点,过P点引x、y轴的平行线交双曲线C2于A、B两点,连接AB.
,且k1>k2>0,点P是双曲线C1上的一点,过P点引x、y轴的平行线交双曲线C2于A、B两点,连接AB.