Question

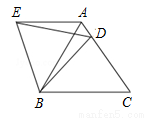
(10分)如图，△ABC中，∠C＝2∠A，BD平分∠ABC交AC于D，求证：AB＝CD＋BC．

 

 

 

Answer 1

见解析

【解析】

试题分析：方法一：(截长法)在AB上取BE＝BC，再证AE＝DE＝CD即可．方法二：(补短法)延长BC至F，使BF=BA，证△BDA≌△BDF，DC＝CF即可

试题解析：方法一：∵∠C=2∠A

∴BC<BA

将ΔBCD沿BD翻折，

∵∠DBC=∠DBA

∴BC落在BA边上为BC.

∴∠BC＇D=∠C=∠A+∠ADC＇，C＇D=CD，BC＇=BC

∵∠C=2∠A

∴∠A=∠ADC＇

∴C＇A=C＇D=CD

∴AB=AC＇+C＇B=CD+BC.

方法二：延长BC至F，使BF=BA，并连接DF

又∵∠ABD=∠FBD，BD=BD

∴ΔABD≌ΔFBD

∴∠A=∠F

∵∠BCD=2∠A=∠F+∠FDC

∴∠F=∠FDC

∴CD=CF

∴AB=BF=BC+CF=BC+CD

即AB=CD+BC.

考点：三角形全等的判定和性质