Question

(12分)如图，AB＝AC，AE＝AF，∠BAC＝∠EAF＝90°，BE、CF交于M，连AM．

⑴求证：BE＝CF；⑵求证：BE⊥CF；⑶求∠AMC的度数．

 

 

Answer 1

(1)见解析；（2）见解析；（3）135°

【解析】

试题分析：⑴证△BEA≌△CFA．⑵∠ABE＝∠ACF，∴∠CMB＝∠CAB＝90°．

⑶作AG⊥BE于G，AH⊥CF于H，证△AGB≌△AHC，AG＝AH，∠AMG＝45°，可得∠AMC＝135°

试题解析：（1）∵∠BAC=∠EAF=90°

∴∠BAE=∠CAF

∵ AE=AF，AB=AC，

∴三角形BAE 全等于 三角形CAF，

∴ BE=CF

（2）∵∠AEB=∠AFC

设CF与AE相交于点H 则∠MHE = ∠AHF

∵三角形EMH与三角形 HAF的内角和都为180°

∴ ∠EMF = ∠EAF

即BE⊥CF

（3）∵∠ABE=∠ACF

∴ A，B，C，M四点共圆

∴ ∠AMC+∠ABC=180°

∵AB=AC，∠BAC=90°,∠ABC=45°

∴ ∠AMC=180°--∠ABC=135°

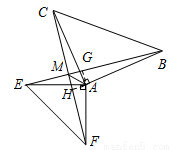
也可以作AG⊥BE于G，AH⊥CF于H，证△AGB≌△AHC，AG＝AH，∠AMG＝45°，可得∠AMC＝135.

考点：