题目内容
【题目】（1）根据下表回答：
| 1 | 1.7 | 1.73 | 1.74 | 1.8 | 2 |
| 1 | 2.89 | 2.9929 | 3.0276 | 3.24 | 4 |
①
的平方根是_____________；
②由表可知，
在表中哪两个相邻的数之间（小数部分是两位小数）？
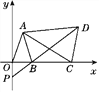
（2）如图，在平面直角坐标系中，已知三点
①三角形
的面积是_______
②分别将
三点的横坐标乘
，纵坐标加
，记坐标变换后所对的点分别为
在坐标系中画出以这三点为顶点的三角形
【答案】(1) ①
；②
在1.73与1.74之间；
(2) ①5.5；②见解析；
【解析】
(1) ①根据平方根的定义，由表格的信息即可得到；
②观察表格的数据，即可得到答案；
(2) ①先观察三角形在直角坐标系中的位置，再用一个矩形的面积减掉多余的三角形的面积即可得到；
②根据题意做变换，即可得到
点变换后的坐标，再在直角坐标系中画出来即可；
解：(1)①由表格可以看出
所对应的x值为1.8
∴3.24的平方根是
②由表格可知，在1.73与1.74之间.
(2)①
故答案为5.5
②D点横坐标为：
，纵坐标为：
∴
E点横坐标为：
，纵坐标为：
∴
F点横坐标为：
，纵坐标为：
∴
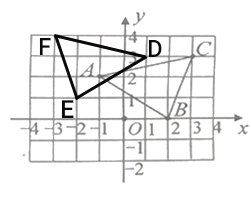
根据得到的点
的坐标在坐标系中画出以这三点为顶点的三角形
如下图：
【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况，根据以往的学习经验，他想到了方程与函数的关系，一次函数y=kx+b（k≠0）的图象与x轴交点的横坐标即为一元一次方程kx+b（k≠0）的解，二次函数y=ax2+bx+c（a≠0）的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0（a≠0）的解，如：二次函数y=x2﹣2x﹣3的图象与x轴的交点为（﹣1，0）和（3，0），交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解． 根据以上方程与函数的关系，如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标，即可知方程x3+2x2﹣x﹣2=0的解．
佳佳为了解函数y=x3+2x2﹣x﹣2的图象，通过描点法画出函数的图象．
x | … | ﹣3 | ﹣ | ﹣2 | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| 2 | … |
y | … | ﹣8 | ﹣ | 0 |
| m | ﹣ | ﹣2 | ﹣ | 0 |
| 12 | … |
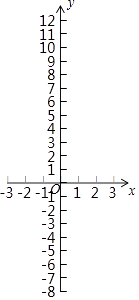
（1）直接写出m的值，并画出函数图象；
（2）根据表格和图象可知，方程的解有个，分别为；
（3）借助函数的图象，直接写出不等式x3+2x2＞x+2的解集．