题目内容
19.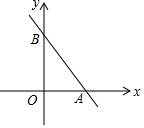 如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,3).
如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,3).(1)求直线AB所对应的函数表达式.
(2)点C在直线AB上,且到y轴的距离是1,求点C的坐标.
分析 (1)设出函数解析式,将两点代入,运用待定系数法求解;
(2)分两种情况:①x=1;②x=-1;代入直线AB所对应的函数表达式可求点C的坐标.
解答 解:(1)设直线AB所对应的函数表达式为y=kx+b,依题意有
$\left\{\begin{array}{l}{2k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=3}\end{array}\right.$.
故函数解析式为:y=-$\frac{3}{2}$x+3;
(2)①x=1时,y=-$\frac{3}{2}$+3=$\frac{3}{2}$;
②x=-1时,y=$\frac{3}{2}$+3=$\frac{9}{2}$.
故点C的坐标为(1,$\frac{3}{2}$)或(-1,$\frac{9}{2}$).
点评 本题考查待定系数法求函数解析式及一次函数图象上点的坐标特征,难度不大,注意掌握待定系数法的运用.

练习册系列答案
相关题目
9.学校购回一批足球,为检测其质量,从中随机抽取8个足球,记录其质量如下表:
则估计这批足球的平均质量和这组数据的方差分别是( )
| 质量(g) | 410 | 420 | 430 | 440 | 450 |
| 个数 | 2 | 1 | 1 | 3 | 1 |
| A. | 430,20 | B. | 430,200 | C. | 440,30 | D. | 440,300 |
 如图,点A的坐标为(-5,0),直线y=$\sqrt{3}$x+t与坐标轴交于点B,C,连结AC,如果∠ACD=90°,则t=-$\frac{5\sqrt{3}}{3}$.
如图,点A的坐标为(-5,0),直线y=$\sqrt{3}$x+t与坐标轴交于点B,C,连结AC,如果∠ACD=90°,则t=-$\frac{5\sqrt{3}}{3}$.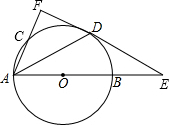 如图,AB是⊙O的直径,且AB=6,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
如图,AB是⊙O的直径,且AB=6,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.