题目内容
(2012•深圳)如图,在平面直角坐标系中,直线l:y=-2x+b(b≥0)的位置随b的不同取值而变化.
(1)已知⊙M的圆心坐标为(4,2),半径为2.
当b=
当b=
(2)若把⊙M换成矩形ABCD,其三个顶点坐标分别为:A(2,0)、B(6,0)、C(6,2).设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式.
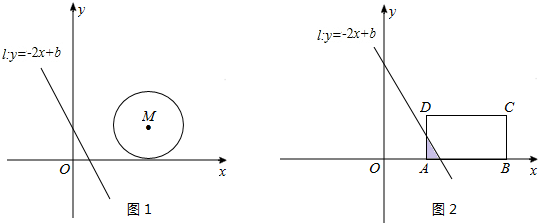
(1)已知⊙M的圆心坐标为(4,2),半径为2.
当b=
10
10
时,直线l:y=-2x+b(b≥0)经过圆心M;当b=
10±2
| 5 |
10±2
时,直线l:y=-2x+b(b≥0)与⊙M相切;| 5 |
(2)若把⊙M换成矩形ABCD,其三个顶点坐标分别为:A(2,0)、B(6,0)、C(6,2).设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式.
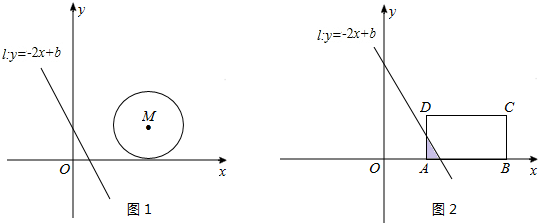
分析:(1)①当直线经过圆心M(4,2)时,将圆心坐标代入直线解析式,即可求得b的值;
②当若直线与⊙M相切,如答图1所示,应有两条符合条件的切线,不要遗漏.
欲求此时b的值,可以先求出切点P的坐标,代入解析式即可;欲求切点P的坐标,可以构造相似三角形△PMN∽△BAO,求得PN=2MN,然后在Rt△PMN中利用勾股定理求出MN和PN,最后求出P点坐标;
(2)本问关键是弄清直线扫过矩形ABCD的运动过程,可以分为五个阶段,分别求出每一阶段S的表达式,如答图2-4所示.
②当若直线与⊙M相切,如答图1所示,应有两条符合条件的切线,不要遗漏.
欲求此时b的值,可以先求出切点P的坐标,代入解析式即可;欲求切点P的坐标,可以构造相似三角形△PMN∽△BAO,求得PN=2MN,然后在Rt△PMN中利用勾股定理求出MN和PN,最后求出P点坐标;
(2)本问关键是弄清直线扫过矩形ABCD的运动过程,可以分为五个阶段,分别求出每一阶段S的表达式,如答图2-4所示.
解答: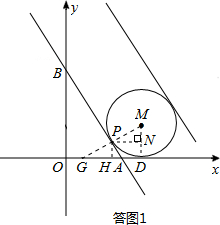 解:(1)①直线l:y=-2x+b(b≥0)经过圆心M(4,2)时,则有:2=-2×4+b,∴b=10;
解:(1)①直线l:y=-2x+b(b≥0)经过圆心M(4,2)时,则有:2=-2×4+b,∴b=10;
②若直线l:y=-2x+b(b≥0)与⊙M相切,如答图1所示,应有两条符合条件的切线.
设直线与x轴、y轴交于A、B点,则A(
,0)、B(0,b),∴OB=2OA.
由题意,可知⊙M与x轴相切,设切点为D,连接MD;
设直线与⊙M的一个切点为P,连接MP并延长交x轴于点G;
过P点作PN⊥MD于点N,PH⊥x轴于点H.
易证△PMN∽△BAO,
∴PN:MN=OB:OA=2:1,
∴PN=2MN.
在Rt△PMN中,由勾股定理得:PM2=PN2+MN2,解得:MN=
,PN=
,
∴PH=ND=MD-MN=2-
,OH=OD-HD=OD-PN=4-
,
∴P(4-
,2-
),代入直线解析式求得:b=10-2
;
同理,当切线位于另外一侧时,可求得:b=10+2
.
(2)由题意,可知矩形ABCD顶点D的坐标为(2,2).
由一次函数的性质可知,当b由小到大变化时,直线l:y=-2x+b(b≥0)向右平移,依次扫过矩形ABCD的不同部分.
可得当直线经过A(2,0)时,b=4;当直线经过D(2,2)时,b=6;当直线经过B(6,0)时,b=12;当直线经过C(6,2)时,b=14.
①当0≤b≤4时,S=0;
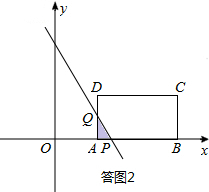
②当4<b≤6时,如答图2所示.
设直线l:y=-2x+b与x轴交于点P,与AD交于点Q.
令y=0,可得x=
,∴AP=
-2;
令x=2,可得y=b-4,∴AQ=b-4.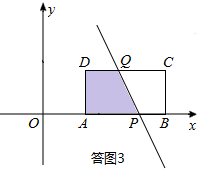
∴S=S△APQ=
AP•AQ=
(
-2)(b-4)=
b2-2b+4;
③当6<b≤12时,如答图3所示.
设直线l:y=-2x+b与x轴交于点P,与CD交于点Q.
令y=0,可得x=
,∴AP=
-2;
令y=2,可得x=
-1,∴DQ=
-3.
S=S梯形APQD=
(DQ+AP)•AD=b-5;
④当12<b≤14时,如答图4所示.
设直线l:y=-2x+b与BC交于点P,与CD交于点Q.
令x=6,可得y=b-12,∴BP=b-12,CP=14-b;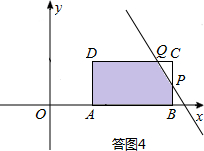
令y=2,可得x=
-1,∴DQ=
-3,CQ=7-
.
S=S矩形ABCD-S△PQC=8-
CP•CQ=-
b2+7b-41;
⑤当b>14时,S=S矩形ABCD=8.
综上所述,当b由小到大变化时,S与b的函数关系式为:
S=
.
 解:(1)①直线l:y=-2x+b(b≥0)经过圆心M(4,2)时,则有:2=-2×4+b,∴b=10;
解:(1)①直线l:y=-2x+b(b≥0)经过圆心M(4,2)时,则有:2=-2×4+b,∴b=10;②若直线l:y=-2x+b(b≥0)与⊙M相切,如答图1所示,应有两条符合条件的切线.
设直线与x轴、y轴交于A、B点,则A(
| b |
| 2 |
由题意,可知⊙M与x轴相切,设切点为D,连接MD;
设直线与⊙M的一个切点为P,连接MP并延长交x轴于点G;
过P点作PN⊥MD于点N,PH⊥x轴于点H.
易证△PMN∽△BAO,
∴PN:MN=OB:OA=2:1,
∴PN=2MN.
在Rt△PMN中,由勾股定理得:PM2=PN2+MN2,解得:MN=
| 2 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
∴PH=ND=MD-MN=2-
| 2 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
∴P(4-
| 4 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
| 5 |
同理,当切线位于另外一侧时,可求得:b=10+2
| 5 |

(2)由题意,可知矩形ABCD顶点D的坐标为(2,2).
由一次函数的性质可知,当b由小到大变化时,直线l:y=-2x+b(b≥0)向右平移,依次扫过矩形ABCD的不同部分.
可得当直线经过A(2,0)时,b=4;当直线经过D(2,2)时,b=6;当直线经过B(6,0)时,b=12;当直线经过C(6,2)时,b=14.
①当0≤b≤4时,S=0;
②当4<b≤6时,如答图2所示.
设直线l:y=-2x+b与x轴交于点P,与AD交于点Q.
令y=0,可得x=
| b |
| 2 |
| b |
| 2 |
令x=2,可得y=b-4,∴AQ=b-4.

∴S=S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| 2 |
| 1 |
| 4 |
③当6<b≤12时,如答图3所示.
设直线l:y=-2x+b与x轴交于点P,与CD交于点Q.
令y=0,可得x=
| b |
| 2 |
| b |
| 2 |
令y=2,可得x=
| b |
| 2 |
| b |
| 2 |
S=S梯形APQD=
| 1 |
| 2 |
④当12<b≤14时,如答图4所示.
设直线l:y=-2x+b与BC交于点P,与CD交于点Q.
令x=6,可得y=b-12,∴BP=b-12,CP=14-b;

令y=2,可得x=
| b |
| 2 |
| b |
| 2 |
| b |
| 2 |
S=S矩形ABCD-S△PQC=8-
| 1 |
| 2 |
| 1 |
| 4 |
⑤当b>14时,S=S矩形ABCD=8.
综上所述,当b由小到大变化时,S与b的函数关系式为:
S=
|
点评:本题是动线型压轴题,综合考查了一次函数的图象与性质、圆的切线性质、相似三角形、矩形、梯形、勾股定理以及图形面积等重要知识点,涉及的考点较多,难度较大,对同学们的解题能力提出了很高的要求.本题的难点在于:(I)第(1)②问中,圆的切线有两条,容易遗漏.求切点坐标时候,注意运用相似关系化简运算;(II)第(2)问中,动直线的运动过程分析是难点,注意划分为五个阶段,分别求出每个阶段S的表达式.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
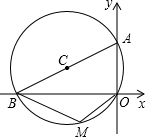 (2012•深圳)如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内
(2012•深圳)如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内
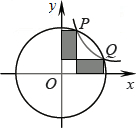 (2012•深圳)如图,双曲线y=
(2012•深圳)如图,双曲线y=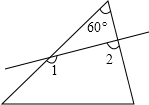 (2012•深圳)如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
(2012•深圳)如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( ) (2012•深圳)如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
(2012•深圳)如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6 (2012•深圳)如图,已知△ABC的三个顶点坐标分别为A(-4,0)、B(1,0)、C(-2,6).
(2012•深圳)如图,已知△ABC的三个顶点坐标分别为A(-4,0)、B(1,0)、C(-2,6).