题目内容
 (2012•深圳)如图,已知△ABC的三个顶点坐标分别为A(-4,0)、B(1,0)、C(-2,6).
(2012•深圳)如图,已知△ABC的三个顶点坐标分别为A(-4,0)、B(1,0)、C(-2,6).(1)求经过A、B、C三点的抛物线解析式;
(2)设直线BC交y轴于点E,连接AE,求证:AE=CE;
(3)设抛物线与y轴交于点D,连接AD交BC于点F,试问以A、B、F为顶点的三角形与△ABC相似吗?
分析:(1)利用待定系数发求解即可得出抛物线的解析式;
(2)求出直线BC的函数解析式,从而得出点E的坐标,然后分别求出AE及CE的长度即可证明出结论;
(3)求出AD的函数解析式,然后结合直线BC的解析式可得出点F的坐标,由题意得∠ABF=∠CBA,然后判断出
是否等于
即可作出判断.
(2)求出直线BC的函数解析式,从而得出点E的坐标,然后分别求出AE及CE的长度即可证明出结论;
(3)求出AD的函数解析式,然后结合直线BC的解析式可得出点F的坐标,由题意得∠ABF=∠CBA,然后判断出
| BF |
| AB |
| AB |
| BC |
解答:解:(1)设函数解析式为:y=ax2+bx+c,
由函数经过点A(-4,0)、B(1,0)、C(-2,6),
可得
,
解得:
,
故经过A、B、C三点的抛物线解析式为:y=-x2-3x+4;
(2)设直线BC的函数解析式为y=kx+b,
由题意得:
,
解得:
,
即直线BC的解析式为y=-2x+2.
故可得点E的坐标为(0,2),
从而可得:AE=
=2
,CE=
=2
,
故可得出AE=CE;
 (3)相似.理由如下:
(3)相似.理由如下:
设直线AD的解析式为y=kx+b,
则
,
解得:
,
即直线AD的解析式为y=x+4.
联立直线AD与直线BC的函数解析式可得:
,
解得:
,
即点F的坐标为(-
,
),
则BF=
=
,
又∵AB=5,BC=
=3
,
∴
=
,
=
,
∴
=
,
又∵∠ABF=∠CBA,
∴△ABF∽△CBA.
故以A、B、F为顶点的三角形与△ABC相似.
由函数经过点A(-4,0)、B(1,0)、C(-2,6),
可得
|
解得:
|
故经过A、B、C三点的抛物线解析式为:y=-x2-3x+4;
(2)设直线BC的函数解析式为y=kx+b,
由题意得:
|
解得:
|
即直线BC的解析式为y=-2x+2.
故可得点E的坐标为(0,2),
从而可得:AE=
| AO2+OE2 |
| 5 |
| (-2-0)2+(6-2)2 |
| 5 |
故可得出AE=CE;
 (3)相似.理由如下:
(3)相似.理由如下:设直线AD的解析式为y=kx+b,
则
|
解得:
|
即直线AD的解析式为y=x+4.
联立直线AD与直线BC的函数解析式可得:
|
解得:
|
即点F的坐标为(-
| 2 |
| 3 |
| 10 |
| 3 |
则BF=
(-
|
5
| ||
| 3 |
又∵AB=5,BC=
| (-2-1)2+(6-0)2 |
| 5 |
∴
| BF |
| AB |
| ||
| 3 |
| AB |
| BC |
| ||
| 3 |
∴
| BF |
| AB |
| AB |
| BC |
又∵∠ABF=∠CBA,
∴△ABF∽△CBA.
故以A、B、F为顶点的三角形与△ABC相似.
点评:此题属于二次函数的综合题目,涉及了相似三角形的判定与性质、待定系数法求二次函数解析式,两点间的距离公式,解答本题要求我们仔细审题,将所学知识联系起来,综合解答.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
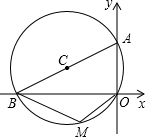 (2012•深圳)如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内
(2012•深圳)如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内
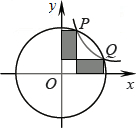 (2012•深圳)如图,双曲线y=
(2012•深圳)如图,双曲线y=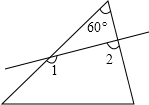 (2012•深圳)如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
(2012•深圳)如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( ) (2012•深圳)如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
(2012•深圳)如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6