题目内容
 如图,已知△ABC是等边三角形,延长BA至E,延长BC至D,使AE=BD,求证:EC=ED.
如图,已知△ABC是等边三角形,延长BA至E,延长BC至D,使AE=BD,求证:EC=ED.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:延长BD至F,使DF=AB,连结EF,就可以得出BE=BF,得出△BEF是等边三角形,就可以得出BE=FE,得出△BCE≌△FDE就可以得出结论.
解答:证明:延长BD至F,使DF=AB,连结EF,
∵△ABC是等边三角形,
∴AB=BC=AC,∠B=60°.
∵AE=BD,DF=AB,
∴AE+AB=BD+DF,
∴BE=BF.
∵∠B=60°,
∴△BEF为等边三角形,
∴∠B=∠F=60°,BE=FE.
∵DF=AB,
∴BC=DF.
在△BCE和△FDE中,
,
∴△BCE≌△FDE(SAS),
∴EC=ED.
∵△ABC是等边三角形,
∴AB=BC=AC,∠B=60°.
∵AE=BD,DF=AB,
∴AE+AB=BD+DF,

∴BE=BF.
∵∠B=60°,
∴△BEF为等边三角形,
∴∠B=∠F=60°,BE=FE.
∵DF=AB,
∴BC=DF.
在△BCE和△FDE中,
|
∴△BCE≌△FDE(SAS),
∴EC=ED.
点评:本题考查了等边三角形的判定及性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明△BEF是等边三角形是关键.正确作辅助线是难点.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 某电信公司开设了甲、乙两种市内移动通信业务.甲种使用者每月需缴18元月租费,然后每通话1分钟,再付话费0.2元;乙种使用者不缴月租费,每通话1分钟,付话费0.6元.若一个月内通话时间为x分钟,甲、乙两种的费用分别为y1和y2元.
某电信公司开设了甲、乙两种市内移动通信业务.甲种使用者每月需缴18元月租费,然后每通话1分钟,再付话费0.2元;乙种使用者不缴月租费,每通话1分钟,付话费0.6元.若一个月内通话时间为x分钟,甲、乙两种的费用分别为y1和y2元.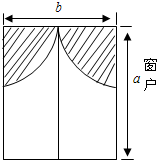 小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成(半径相同,π取3)
小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成(半径相同,π取3)
 要使图中的展开图折叠成正方体后,相对面上两个数之和为5,x=
要使图中的展开图折叠成正方体后,相对面上两个数之和为5,x=