题目内容
解方程:
(1)用配方法解方程:6x2-x-12=0
(2)(x+4)2=5(x+4)
解:(1)x2- x=2,
x=2,
x2- x+(
x+( )2=2+(
)2=2+( )2,
)2,
∵(x- )2=
)2=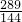
∴x- =±
=±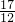
∴x1= ,x2=-
,x2=- ;
;
(2)∵(x+4)2-5(x+4)=0,
∴(x+4)(x+4-5)=0,
∴x+4=0或x+4-5=0,
∴x1=-4,x2=1.
分析:(1)先把二次系数化为1得到x2- x=2,两边加上
x=2,两边加上 的平方后得到(x-
的平方后得到(x- )2=
)2=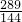 ,然后利用直接开平方法求解;
,然后利用直接开平方法求解;
(2)先移项得到(x+4)2-5(x+4)=0,方程左边分解得(x+4)(x+4-5)=0,原方程化为x+4=0或x+4-5=0,然后解一次方程即可.
点评:本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,再把方程左边分解为两个一次式的乘积,这样原方程转化为两个一元一次方程,然后解一次方程即可得到一元二次方程的解.也考查了配方法解一元二次方程.
 x=2,
x=2,x2-
 x+(
x+( )2=2+(
)2=2+( )2,
)2,∵(x-
 )2=
)2=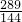
∴x-
 =±
=±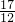
∴x1=
 ,x2=-
,x2=- ;
;(2)∵(x+4)2-5(x+4)=0,
∴(x+4)(x+4-5)=0,
∴x+4=0或x+4-5=0,
∴x1=-4,x2=1.
分析:(1)先把二次系数化为1得到x2-
 x=2,两边加上
x=2,两边加上 的平方后得到(x-
的平方后得到(x- )2=
)2=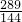 ,然后利用直接开平方法求解;
,然后利用直接开平方法求解;(2)先移项得到(x+4)2-5(x+4)=0,方程左边分解得(x+4)(x+4-5)=0,原方程化为x+4=0或x+4-5=0,然后解一次方程即可.
点评:本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,再把方程左边分解为两个一次式的乘积,这样原方程转化为两个一元一次方程,然后解一次方程即可得到一元二次方程的解.也考查了配方法解一元二次方程.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目