题目内容
如图①,②,在平面直角坐标系 中,点
中,点 的坐标为(4,0),以点
的坐标为(4,0),以点 为圆心,
为圆心,4为半径的圆与
 轴交于
轴交于 ,
, 两点,
两点, 为弦,
为弦, ,
, 是
是 轴上的一动点,连结
轴上的一动点,连结 .
.
(1)求
 的度数;(2分)
的度数;(2分)(2)如图①,当
 与⊙A相切时,求
与⊙A相切时,求 的长;(2分)
的长;(2分)(3)如图②,当点
 在直径
在直径 上时,
上时, 的延长线与⊙A相交于点
的延长线与⊙A相交于点 ,问
,问 为何值时,
为何值时, 是等腰三角形?(5分)
是等腰三角形?(5分)
解:(1)∵ ,
, ,
,
∴ 是等边三角形. ∴
是等边三角形. ∴ .
.
(2)∵CP与⊙A相切,∴ .
.
∴ .……………3分
.……………3分
又∵ (4,0),∴
(4,0),∴ .∴
.∴ .
.
∴ . ………4分
. ………4分
(3)①过点 作
作 ,垂足为
,垂足为 ,延长
,延长 交⊙A于
交⊙A于 ,
,

∵ 是半径,∴CP1=Q1P1,∴
是半径,∴CP1=Q1P1,∴ ,
,
∴ 是等腰三角形.…………………………5分
是等腰三角形.…………………………5分
又∵ 是等边三角形,∴
是等边三角形,∴ ="2" .……6分
="2" .……6分
②解法一:过 作
作 ,垂足为
,垂足为 ,延长
,延长 交⊙A于
交⊙A于 ,
, 与
与 轴
轴
交于 ,∵
,∵ 是圆心,∴
是圆心,∴ 是
是 的垂直平分线.∴
的垂直平分线.∴ .
.
∴ 是等腰三角形,………………………………7分
是等腰三角形,………………………………7分
过点 作
作 轴于
轴于 ,在
,在 中,
中,
∵ ,
,
∴ .∴点
.∴点 的坐标(4+
的坐标(4+ ,
, ).
).
在 中,∵
中,∵ ,
,
∴ .∴
.∴ 点坐标(2,
点坐标(2, ).…………………8分
).…………………8分
设直线 的关系式为:
的关系式为: ,则有:
,则有:
解得: ∴
∴ .
.
当 时,
时, .∴
.∴
解法二:过A作 ,垂足为
,垂足为 ,延长
,延长 交⊙A于
交⊙A于 ,
,
 与
与 轴交于
轴交于 ,∵
,∵ 是圆心,
是圆心,
∴ 是
是 的垂直平分线.∴
的垂直平分线.∴ .∴
.∴ 是等腰三角形.
是等腰三角形.
∵ ,∴
,∴ .
.
∵ 平分
平分 ,∴
,∴ .
.
∵ 是等边三角形,
是等边三角形, ,∴
,∴ .
.
∴ .
.
∴ 是等腰直角三角形.∴
是等腰直角三角形.∴ .
.
∴ .解析:
.解析:
略
 ,
, ,
,∴
 是等边三角形. ∴
是等边三角形. ∴ .
.(2)∵CP与⊙A相切,∴
 .
. ∴
 .……………3分
.……………3分又∵
 (4,0),∴
(4,0),∴ .∴
.∴ .
.∴
 . ………4分
. ………4分(3)①过点
 作
作 ,垂足为
,垂足为 ,延长
,延长 交⊙A于
交⊙A于 ,
,
∵
 是半径,∴CP1=Q1P1,∴
是半径,∴CP1=Q1P1,∴ ,
,∴
 是等腰三角形.…………………………5分
是等腰三角形.…………………………5分又∵
 是等边三角形,∴
是等边三角形,∴ ="2" .……6分
="2" .……6分②解法一:过
 作
作 ,垂足为
,垂足为 ,延长
,延长 交⊙A于
交⊙A于 ,
, 与
与 轴
轴交于
 ,∵
,∵ 是圆心,∴
是圆心,∴ 是
是 的垂直平分线.∴
的垂直平分线.∴ .
.∴
 是等腰三角形,………………………………7分
是等腰三角形,………………………………7分过点
 作
作 轴于
轴于 ,在
,在 中,
中,∵
 ,
,∴
 .∴点
.∴点 的坐标(4+
的坐标(4+ ,
, ).
).在
 中,∵
中,∵ ,
,∴
 .∴
.∴ 点坐标(2,
点坐标(2, ).…………………8分
).…………………8分设直线
 的关系式为:
的关系式为: ,则有:
,则有:
解得:
 ∴
∴ .
.当
 时,
时, .∴
.∴
解法二:过A作
 ,垂足为
,垂足为 ,延长
,延长 交⊙A于
交⊙A于 ,
, 与
与 轴交于
轴交于 ,∵
,∵ 是圆心,
是圆心,∴
 是
是 的垂直平分线.∴
的垂直平分线.∴ .∴
.∴ 是等腰三角形.
是等腰三角形.∵
 ,∴
,∴ .
.∵
 平分
平分 ,∴
,∴ .
.∵
 是等边三角形,
是等边三角形, ,∴
,∴ .
.∴
 .
.∴
 是等腰直角三角形.∴
是等腰直角三角形.∴ .
.∴
 .解析:
.解析:略

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
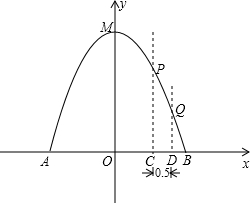 的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.
的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系. 水柱在与池中心的水平距离为1m处达到最高,高度为3m.
水柱在与池中心的水平距离为1m处达到最高,高度为3m.




