题目内容
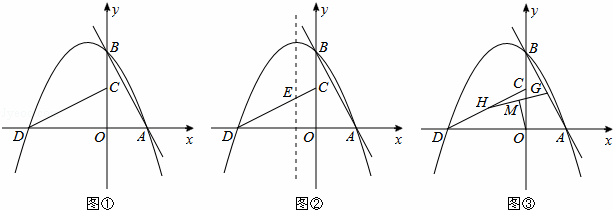
如图①,直线l:y=mx+n(m>0,n<0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°,得到△COD,过点A,B,D的抛物线P叫做l的关联抛物线,而l叫做P的关联直线.
(1)若l:y=﹣2x+2,则P表示的函数解析式为 ;若P:y=﹣x2﹣3x+4,则l表示的函数解析式为 .
(2)求P的对称轴(用含m,n的代数式表示);
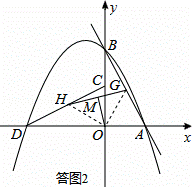
(3)如图②,若l:y=﹣2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;
(4)如图③,若l:y=mx﹣4m,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=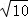 ,直接写出l,P表示的函数解析式.
,直接写出l,P表示的函数解析式.
解:(1)若l:y=﹣2x+2,则A(1,0),B(0,2).
∵将△AOB绕点O逆时针旋转90°,得到△COD,
∴D(﹣2,0).
设P表示的函数解析式为:y=ax2+bx+c,将点A、B、D坐标代入得:
 ,解得
,解得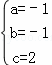 ,
,
∴P表示的函数解析式为:y=﹣x2﹣x+2;
若P:y=﹣x2﹣3x+4=﹣(x+4)(x﹣1),则D(﹣4,0),A(1,0).
∴B(0,4).
设l表示的函数解析式为:y=kx+b,将点A、B坐标代入得:
 ,解得
,解得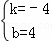 ,
,
∴l表示的函数解析式为:y=﹣4x+4.
(2)直线l:y=mx+n(m>0,n<0),
令y=0,即mx+n=0,得x=﹣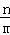 ;令x=0,得y=n.
;令x=0,得y=n.
∴A(﹣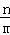 ,0)、B(0,n),
,0)、B(0,n),
∴D(﹣n,0).
设抛物线对称轴与x轴的交点为N(x,0),
∵DN=AN,∴﹣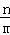 ﹣x=x﹣(﹣n),
﹣x=x﹣(﹣n),
∴2x=﹣n﹣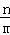 ,
,
∴P的对称轴为x=﹣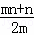 .
.
(3)若l:y=﹣2x+4,则A(2,0)、B(0,4),
∴C(0,2)、D(﹣4,0).
可求得直线CD的解析式为:y=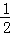 x+2.
x+2.
由(2)可知,P的对称轴为x=﹣1.
∵以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形,
∴FQ∥CE,且FQ=CE.
设直线FQ的解析式为:y=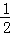 x+b.
x+b.
∵点E、点C的横坐标相差1,∴点F、点Q的横坐标也是相差1.
则|xF﹣(﹣1)|=|xF+1|=1,
解得xF=0或xF=﹣2.
∵点F在直线ll:y=﹣2x+4上,∴点F坐标为(0,4)或(﹣2,8).
若F(0,4),则直线FQ的解析式为:y=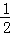 x+4,当x=﹣1时,y=
x+4,当x=﹣1时,y=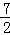 ,∴Q1(﹣1,
,∴Q1(﹣1,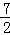 );
);
若F(﹣2,8),则直线FQ的解析式为:y=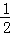 x+9,当x=﹣1时,y=
x+9,当x=﹣1时,y=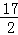 ,∴Q2(﹣1,
,∴Q2(﹣1,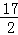 ).
).
∴满足条件的点Q有2个,如答图1所示,点Q坐标为Q1(﹣1,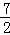 )、Q2(﹣1,
)、Q2(﹣1,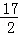 ).
).
(4)如答图2所示,连接OG、OH.
∵点G、H为斜边中点,∴OG=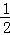 AB,OH=
AB,OH=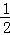 CD.
CD.
由旋转性质可知,AB=CD,OG⊥OH,
∴△OGH为等腰直角三角形.
∵点G为GH中点,∴△OMG为等腰直角三角形,
∴OG=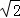 OM=
OM=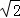 •
•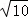 =2
=2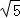 ,
,
∴AB=2OG=4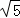 .
.
∵l:y=mx﹣4m,∴A(4,0),B(0,﹣4m).
在Rt△AOB中,由勾股定理得:OA2+OB2=AB2,即:42+(﹣4m)2=(4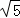 )2,
)2,
解得:m=﹣2或m=2,
∵点B在y轴正半轴,∴m=2舍去,∴m=﹣2.
∴l表示的函数解析式为:y=﹣2x+4;
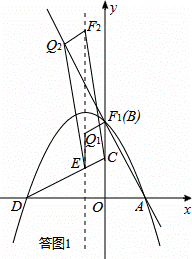
∴B(0,8),D(﹣8,0).又A(4,0),利用待定系数法求得P:y=﹣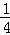 x2﹣x+8.
x2﹣x+8.

若 +(y+2)2=0,则(x+y)2014等于( )
+(y+2)2=0,则(x+y)2014等于( )
|
| A. | ﹣1 | B. | 1 | C. | 32014 | D. | ﹣32014 |
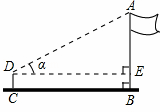
某校九年级四个数学活动小组参加测量操场旗杆高度的综合时间活动,如图是四个小组在不同位置测量后绘制的示意图,用测角仪测得旗杆顶端A的仰角级记为α,CD为测角仪的高,测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB,四个小组测量和计算数据如下表所示:
| 组别数据 | CD的长(m) | BC的长(m) | 仰角α | AB的长(m) |
| 第一组 | 1.59 | 1.32 | 32° | 9.8 |
| 第二组 | 1.54 | 13.4 | 31° | 9.6 |
| 第三组 | 1.57 | 14.1 | 30° | 9.7 |
| 第四组 | 1.56 | 15.2 | 28° |
(1)利用第四组学生测量的数据,求旗杆AB的高度(精确到0.1m);
(2)四组学生测量旗杆高度的平均值为 m(精确到0.1m).
 次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.
次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.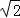 ≈1.41,
≈1.41,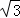 ≈1.73,
≈1.73,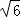 ≈2.45)
≈2.45)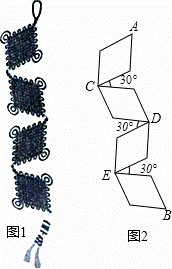
 和
和 都经过圆心O,则阴影部分的面积是 (结果保留π)
都经过圆心O,则阴影部分的面积是 (结果保留π)

 的解集是 。
的解集是 。
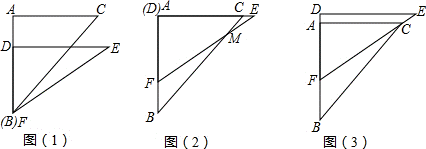
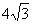 。 将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
。 将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.