题目内容
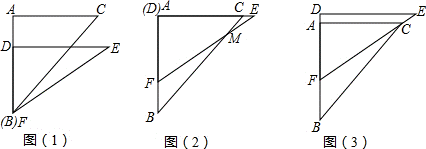
有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=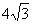 。 将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
。 将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
(1)如图(3),在三角板DEF;运动过程中,当EF经过点C时,∠FCB= 度;BF= ;
(2)如图(2)在三角板DEF运动过程中,EF与BC交于点M,过点M做MN⊥AB于点N,设BF=x,用x的代数式表示MN;
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x的取值范围.
解:(1)∠FCB=15°;BF=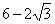
(2)因为MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN
又∵NF=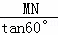 =
=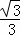 MN,BN=NF+BF,
MN,BN=NF+BF,
 ∴NF+BF=MN,即
∴NF+BF=MN,即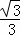 MN+x=MN,解得:MN=
MN+x=MN,解得:MN=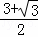 x.
x.
(3)在三角板DEF运动过程中,
(I)当0≤x≤2时,如答图1所示:
y=S△BDG﹣S△BFM
=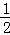 BD•DG﹣
BD•DG﹣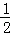 BF•MN
BF•MN
=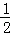 (x+4)2﹣
(x+4)2﹣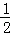 x•
x•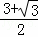 x
x
=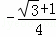 x2+4x+8;
x2+4x+8;
(II)当2<x≤6﹣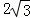 时,如答图2所示:
时,如答图2所示:
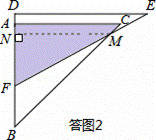 y=S△ABC﹣S△BFM
y=S△ABC﹣S△BFM
=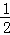 AB•AC﹣
AB•AC﹣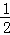 BF•MN
BF•MN
=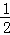 ×62﹣
×62﹣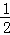 x•
x•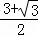 x
x
=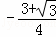 x2+18;
x2+18;
 (III)当6﹣
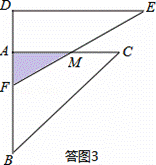
(III)当6﹣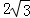 <x≤6时,如答图3所示:
<x≤6时,如答图3所示:
由BF=x,则AF=AB﹣BF=6﹣x,
设AC与EF交于点M,则AM=AF•tan60°=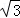 (6﹣x).
(6﹣x).
y=S△AFM=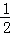 AF•AM=
AF•AM=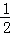 (6﹣x)•
(6﹣x)•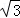 (6﹣x)
(6﹣x)
=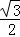 x2﹣
x2﹣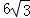 x+
x+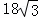 .
.
综上所述,y与x的函数解析式为:
y= .
.

若x:y=1:3,2y=3z,则 的值是( )
的值是( )
|
| A. | ﹣5 | B. | ﹣ | C. |
| D. | 5 |
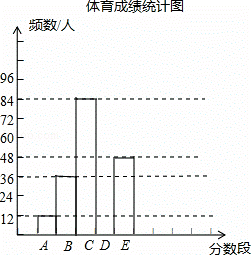
为了了解某市初三年级学生体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计如下体育成绩统计表
| 分数段 | 频数/人 | 频率 |
| A | 12 | 0.05 |
| B | 36 | a |
| C | 84 | 0.35 |
| D | b | 0.25 |
| E | 48 | 0.20 |
根据上面通过的信息,回答下列问题:
(1)统计表中,a= ,b= ,并将统计图补充完整;
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗? (填“正确”或“错误”);
(3)若成绩在27分以上(含27分)定为优秀,则该市今年48000名初三年级学生中体育成绩为优秀的学生人数约有多少?
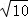 ,直接写出l,P表示的函数解析式.
,直接写出l,P表示的函数解析式.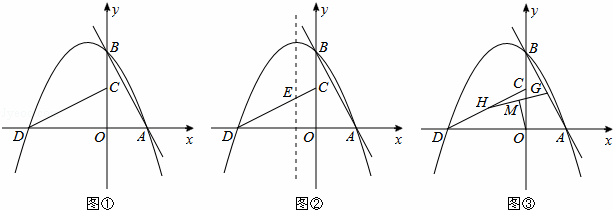
 ,其中
,其中 60°
60°

 30°,请你取一个合适的数作为
30°,请你取一个合适的数作为 如图,由3×3组成的方格中每个方格内均有代数式(图中只列出了部分代数式),方格中每一行、每一列以及每一条对角线上的三个代数式的和均相等。求打上“a”的方格内的数。
如图,由3×3组成的方格中每个方格内均有代数式(图中只列出了部分代数式),方格中每一行、每一列以及每一条对角线上的三个代数式的和均相等。求打上“a”的方格内的数。 的解集在数轴上表示正确的是 ( )
的解集在数轴上表示正确的是 ( ) 
 的解是 ;
的解是 ; 