题目内容
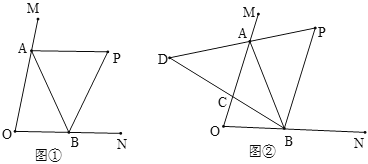
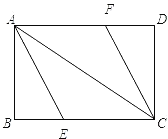
【题目】如图,![]() ,
,![]() 分别平分
分别平分![]() 的外角
的外角![]() 、内角
、内角![]() 、外角
、外角![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的结论有( ).
.其中正确的结论有( ).

A.1个B.2个C.3个D.4个
【答案】D
【解析】
根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EAC=∠ABC+∠ACB=2∠ABC,根据角平分线的定义可得∠EAC=2∠EAD,然后求出∠EAD=∠ABC,再根据同位角相等,两直线平行可得AD∥BC,判断出①正确;
根据两直线平行,内错角相等可得∠ADB=∠CBD,再根据角平分线的定义可得∠ABC=2∠CBD,从而得到∠ACB=2∠ADB,判断出②正确;
根据两直线平行,内错角相等可得∠ADC=∠DCF,再根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义整理可得∠ADC=90°-∠ABD,判断出④正确;
根据三角形的外角性质与角平分线的定义表示出∠DCF,然后整理得到∠BDC=![]() ∠BAC,判断出⑤正确;再根据两直线平行,内错角相等可得∠CBD=∠ADB,∠ABC与∠BAC不一定相等,所以∠ADB与∠BDC不一定相等,判断出③错误.
∠BAC,判断出⑤正确;再根据两直线平行,内错角相等可得∠CBD=∠ADB,∠ABC与∠BAC不一定相等,所以∠ADB与∠BDC不一定相等,判断出③错误.
解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
∴∠ACB=2∠ADB,∴②正确;
∵AD∥BC,
∴∠ADC=∠DCF,
∵CD是∠ACF的平分线,
∴∠ADC=![]() ∠ACF=
∠ACF=![]() (∠ABC+∠BAC)=
(∠ABC+∠BAC)=![]() (180°-∠ACB)=
(180°-∠ACB)=![]() (180°-∠ABC)=90°-∠ABD,
(180°-∠ABC)=90°-∠ABD,
∴④正确;
∵∠BDC=∠DCF-∠DBF=![]() ∠ACF-
∠ACF-![]() ∠ABC=
∠ABC=![]() ∠BAC,
∠BAC,
∴⑤正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC=![]() ∠ABC,
∠ABC,
∵∠ADB=∠DBC=![]() ∠ABC,∠BDC=
∠ABC,∠BDC=![]() ∠BAC,
∠BAC,
∵∠ABC与∠BAC不一定相等,
∴∠ADB与∠BDC不一定相等,
∴③错误.
综上所述,结论正确的是①②④⑤共4个.
故选:D.

 名校课堂系列答案
名校课堂系列答案