题目内容
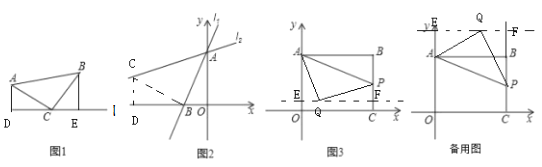
【题目】建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.

(1)操作:
过点A作AD⊥![]() 于点D,过点B作BE⊥
于点D,过点B作BE⊥![]() 于点E.求证:△CAD≌△BCE.
于点E.求证:△CAD≌△BCE.
(2)模型应用:
①如图2,在直角坐标系中,直线![]() :
:![]() 与y轴交于点A,与x轴交于点B,将直线
与y轴交于点A,与x轴交于点B,将直线![]() 绕着点A顺时针旋转45°得到直线
绕着点A顺时针旋转45°得到直线![]() .求直线
.求直线![]() 的函数表达式.
的函数表达式.
②如图3,在直角坐标系中,点B(4,3),作BA⊥y轴于点A,作BC⊥x轴于点C,P是直线BC上的一个动点,点Q(a,5a﹣2)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
【答案】(1)详见解析;(2)![]() (3)
(3)![]() 或
或![]() .
.
【解析】
(1)根据AAS即可证明△DAC≌△ECB;
(2)过点B作BC⊥BA,交直线l2于点C,过点C作CD⊥x轴于点D.根据![]() 得到AO=3,OB=1,根据△DCB≌△OBA可得点C的坐标为(-4,1),再根据待定系数法即可求解;
得到AO=3,OB=1,根据△DCB≌△OBA可得点C的坐标为(-4,1),再根据待定系数法即可求解;
(3)根据题意分两种情况分别作图即可求解.
(1)∵∠ACB=90°,
∴∠ACD+∠BCE=90°
∵AD⊥l,BE⊥l,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠DAC=90° ,
∴∠DAC=∠ECB
∵在△DAC和△ECB中,∠ADC=∠CEB,∠DAC=∠ECB,AC=CB
∴△DAC≌△ECB(AAS)
(2)过点B作BC⊥BA,交直线l2于点C,过点C作CD⊥x轴于点D.
由直线![]() :
:![]() 与y轴交于点A,与x轴交于点B,
与y轴交于点A,与x轴交于点B,
可求点A坐标为(0,3),点B坐标为(-1,0),
∴AO=3,OB=1.
由△DCB≌△OBA可得,DC=OB=1,DB=OA=3,
∴点C的坐标为(-4,1)
设直线m的解析式为:y=kx+b,把(0,3),(-4,1)代入,
求得![]() .
.
(3)如图3,由△AEQ≌△QFP可得AE=QF,3-(5a-2)=4-a,
求得![]() .
.
如备用图,由△AEQ≌△QFP可得AE=QF,(5a-2)-3=4-a,
求得![]() .
.

【题目】(1) 观察被开方数a的小数点与算术平方根![]() 的小数点的移动规律:
的小数点的移动规律:
a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| 0.01 | x | 1 | y | 100 |
填空:x= _______, y=______.
(2)根据你发现的规律填空:
①已知![]() ≈1.414,则
≈1.414,则![]() =________,
=________,![]() =_______;
=_______;
②![]() = 0.274,记
= 0.274,记![]() 的整数部分为x,则
的整数部分为x,则![]() =___________.
=___________.