题目内容
函数y=ax2+c（a≠0）的对称轴是 ；顶点是 ；要使函数y=-mx2开口向上，则 m ．
【答案】分析：由于抛物线顶点式y=a（x-h）2+k，顶点坐标是（h，k），对称轴是x=h，由此可以得到函数y=ax2+c（a≠0）的图象的对称轴，顶点坐标．
已知函数开口向上，二次项系数-m＞0，可求m的范围．
解答：解：根据抛物线顶点式y=a（x-h）2+k，
得函数y=ax2+c（a≠0）的图象的对称轴是y轴，顶点坐标是（0，c）．
∵函数y=-mx2开口向上，
∴-m＞0，即m＜0．
故答案为：y轴，（0，c），＜0．
点评：此题主要考查了二次函数的性质以及抛物线的顶点坐标、对称轴求法，注意二次函数y=ax2+bx+c（a，b，c为常数，a≠0），a决定函数的开口方向．
已知函数开口向上，二次项系数-m＞0，可求m的范围．
解答：解：根据抛物线顶点式y=a（x-h）2+k，
得函数y=ax2+c（a≠0）的图象的对称轴是y轴，顶点坐标是（0，c）．
∵函数y=-mx2开口向上，
∴-m＞0，即m＜0．
故答案为：y轴，（0，c），＜0．
点评：此题主要考查了二次函数的性质以及抛物线的顶点坐标、对称轴求法，注意二次函数y=ax2+bx+c（a，b，c为常数，a≠0），a决定函数的开口方向．
练习册系列答案
相关题目
15、函数y=ax2+bx+c的图象如图所示，且线段OM与ON相等，则a，b，c之间的关系为
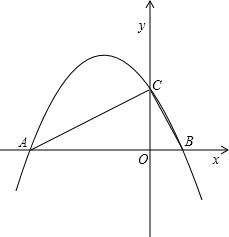如图所示，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于C（0，2），若∠ACB=90°，
如图，二次函数y=ax2+bx+c的图象与x轴交于B、C两点，与y轴交于点A（0，-3），∠ABC=45°，∠ACB=60°，求这个二次函数解析式．
已知正比例函数y=ax与反比例函数
