题目内容
(1)先化简,再求值:
-
÷
,其中a=1-
(2)直线L与直线y=2x+1的交点的横坐标为2,与直线y=-x+2的交点的纵坐标为1,求直线L对应的函数解析式.
| a+1 |
| a-1 |
| a |
| a2-2a+1 |
| 1 |
| a |
| 2 |
(2)直线L与直线y=2x+1的交点的横坐标为2,与直线y=-x+2的交点的纵坐标为1,求直线L对应的函数解析式.
考点:分式的化简求值,两条直线相交或平行问题
专题:计算题
分析:(1)原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,把a的值代入计算即可求出值;
(2)设直线L对应的函数解析式为:y=kx+b(k≠0),把两点坐标代入求出k与b的值,即可确定出解析式.
(2)设直线L对应的函数解析式为:y=kx+b(k≠0),把两点坐标代入求出k与b的值,即可确定出解析式.
解答:解:(1)原式=
-
•a=
=-
,
当a=1-
时,原式=-
;
(2)根据题意得:直线L过(2,5)、(1,1)两点,
设直线L对应的函数解析式为:y=kx+b(k≠0),
把两点坐标代入得:
,
解得:k=4,b=-3,
∴y=4x-3.
| a+1 |
| a-1 |
| a |
| (a-1)2 |
| a2-1-a2 |
| (a-1)2 |
| 1 |
| (a-1)2 |
当a=1-
| 2 |
| 1 |
| 2 |
(2)根据题意得:直线L过(2,5)、(1,1)两点,
设直线L对应的函数解析式为:y=kx+b(k≠0),
把两点坐标代入得:
|
解得:k=4,b=-3,
∴y=4x-3.
点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
我市7月的某一周每天的最高气温(单位:℃)统计如下:34,36,35,36,36,35,33,则这组数据的中位数与众数分别是( )
| A、35,35 |
| B、36,36 |
| C、35,36 |
| D、36,35 |
在一个由8×8个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为S1,把圆周经过的所有小方格的圆外部分的面积之和记为S2,则
的整数部分是 .
| S1 |
| S2 |
下列语句中,正确的是( )
| A、-9的平方根是-3 |
| B、9的平方根是3 |
| C、0没有算术平方根 |
| D、9的算术平方根是3 |
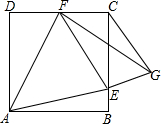 如图,在正方形ABCD中,E、F分别是BC、DC上的两点,若EF=BE+DF.
如图,在正方形ABCD中,E、F分别是BC、DC上的两点,若EF=BE+DF.