题目内容
解方程组
.
|
考点:高次方程
专题:计算题
分析:先变形两个方程得到18b2-4a2=a2b2和b2=20-a2,再利用代入法消去b得18(20-a2)-4a2=a2(20-a2),整理得a4-44a2+160=0,解得a2=40或a2=4,然后计算b2的值,只有易得a和b的值,最后写出原方程组的四组解.
解答:解:
,
由①得18b2-4a2=a2b2③,
由②得b2=20-a2④,
把④代入③得18(20-a2)-4a2=a2(20-a2),
整理得a4-44a2+160=0,解得a2=40或a2=4,
当a2=40,则b2=20-a2=-20,不合题意舍去;
当a2=4,则b2=20-a2=16,
所以a=±2,b=±4,
所以原方程组的解为
或
或
或
.
|
由①得18b2-4a2=a2b2③,
由②得b2=20-a2④,
把④代入③得18(20-a2)-4a2=a2(20-a2),
整理得a4-44a2+160=0,解得a2=40或a2=4,
当a2=40,则b2=20-a2=-20,不合题意舍去;
当a2=4,则b2=20-a2=16,
所以a=±2,b=±4,
所以原方程组的解为
|
|
|
|
点评:本题考查了高次方程:通过适当的方法,把高次方程化为次数较低的方程求解.所以解高次方程一般要降次,即把它转化成二次方程或一次方程.也有的通过因式分解来解.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 如图,点A,B位于直线l同侧,定长为a的线段MN在直线l上滑动,问:当MN滑动到何处时,折线AMNB的长度最短?
如图,点A,B位于直线l同侧,定长为a的线段MN在直线l上滑动,问:当MN滑动到何处时,折线AMNB的长度最短?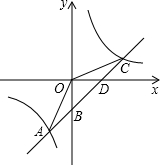 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=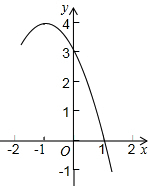 已知抛物线y=-x2+bx-c的部分图象如图所示.
已知抛物线y=-x2+bx-c的部分图象如图所示.