题目内容
如图,在 中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF. 求证:四边形BCFE是菱形.
中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF. 求证:四边形BCFE是菱形.

证明: 、
、 是
是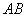 、
、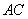 的中点,
的中点,
又
 .
.
 四边形
四边形 是菱形.
是菱形.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
题目内容
如图,在 中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF. 求证:四边形BCFE是菱形.
中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF. 求证:四边形BCFE是菱形.

证明: 、
、 是
是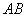 、
、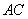 的中点,
的中点,
又
 .
.
 四边形
四边形 是菱形.
是菱形.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案