题目内容
如图，边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上，则△AEF的内切圆半径为
- A.
- B.
- C.
- D.
A
分析：由于△ABC、△EFD都是等边三角形，因此它们的内心重合，设△ABC的内心为M，△AEF的内心为N，连接FN、MF，可先证MN=MF，而后由AN=MA-MN=MA-MF求出MA的值，易知∠NAF=30°，根据直角三角形的性质即可求出△AEF的内切圆半径．
解答：设△AEF的内切圆半径为r，
∵△ABC、△DEF都是等边三角形，且△DEF的三个顶点都在△ABC的边上，
∴△AEF≌△BDE≌△CFD，
∴AF=BE，AE+AF+EF=AE+BE+EF=m+n，
S△ABC=
m2，S△DEF=n2，
∴S△AEF=
（S△ABC-S△DEF）=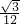
（m2-n2），
则r=
=
（m-n）．
故选A．
点评：此题考查的知识点有：等边三角形的性质、三角形的内切圆、三角形的外角性质以及直角三角形的性质等知识，综合性强，难度较大．
分析：由于△ABC、△EFD都是等边三角形，因此它们的内心重合，设△ABC的内心为M，△AEF的内心为N，连接FN、MF，可先证MN=MF，而后由AN=MA-MN=MA-MF求出MA的值，易知∠NAF=30°，根据直角三角形的性质即可求出△AEF的内切圆半径．
解答：设△AEF的内切圆半径为r，
∵△ABC、△DEF都是等边三角形，且△DEF的三个顶点都在△ABC的边上，
∴△AEF≌△BDE≌△CFD，
∴AF=BE，AE+AF+EF=AE+BE+EF=m+n，
S△ABC=
m2，S△DEF=n2，∴S△AEF=
（S△ABC-S△DEF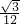）=（m2-n2），则r=
=（m-n）．故选A．
点评：此题考查的知识点有：等边三角形的性质、三角形的内切圆、三角形的外角性质以及直角三角形的性质等知识，综合性强，难度较大．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
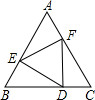如图，边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上，则△AEF的内切圆半径为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
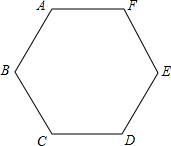已知：如图，边长为a的正六边形ABCDEF．
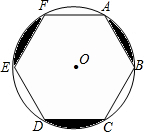如图，边长为2的正六边形ABCDEF内接于⊙O，则图中阴影部分的面积为
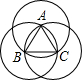如图，边长为1的正△ABC，分别以顶点A，B，C为圆心，1为半径作圆，那么这三个圆所覆盖的图形面积为
如图，边长为1的正六边形纸片是轴对称图形，它的对称轴的条数是（ ）