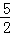题目内容
如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,在射线AN上取一点C,使得DC=DB,问∠ABD与∠ACD有什么数量关系?请说明理由.

考点: 全等三角形的判定与性质.
分析: 分两种情况:当点C在线段AF上,Rt△DEB≌Rt△DFC,可证得∠ABD=∠ACD;当点C在线段AF的延长线上时,Rt△DEB≌Rt△DFC,可证得∠ABD+∠ACD=180°.
解答: 解:∠ABD=∠ACD或∠ABD+∠ACD=180°;
分两种情况:
①如图1,当点C在线段AF上时,
∵DE⊥AM于E,DF⊥AN于F,
∴∠DEB=∠DFC=90°,
在Rt△DEB和Rt△DFC中,
 ,
,
∴Rt△DEB≌Rt△DFC,
∴∠DBE=∠DCF,
∴∠ABD=∠ACD;
②如图2,当点C在线段AF的延长线上时,
同理可证Rt△DEB≌Rt△DFC,
∴∠DBE=∠DCF,
∵∠DBE+∠ABD=180°,
∴∠ABD+∠ACD=180°.


点评: 本题主要考查了全等三角形的判定与性质,全面思考问题,意识到有两种情形是正确解答的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
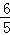 B. 2 C.
B. 2 C. 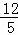 D.
D.