题目内容
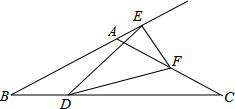 已知:如图,在△ABC中,AB=AC,BC为最大边,点D、F分别在BC、AC上.BD=CF,E为BA延长线上一点.若∠B=∠EDF=∠C=30°,求∠DEF的度数.
已知:如图,在△ABC中,AB=AC,BC为最大边,点D、F分别在BC、AC上.BD=CF,E为BA延长线上一点.若∠B=∠EDF=∠C=30°,求∠DEF的度数.考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:
分析:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EDC=∠BED+∠B,然后求出∠BED=∠CDF,再利用“角角边”证明△BDE和△CFD全等,根据全等三角形对应边相等可得DE=DF,再利用等腰三角形两底角相等列式计算即可得解.
解答:解:∵∠EDC=∠BED+∠B=∠EDF+∠CDF,∠B=∠EDF=30°,
∴∠BED=∠CDF,
在△BDE和△CFD中,
,
∴△BDE≌△CFD(AAS),
∴DE=DF,
∵∠EDF=30°,
∴∠DEF=
(180°-30°)=75°.
∴∠BED=∠CDF,
在△BDE和△CFD中,
|
∴△BDE≌△CFD(AAS),
∴DE=DF,
∵∠EDF=30°,
∴∠DEF=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定与性质,等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并求出∠BED=∠CDF是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 在任意三角形ABC边上画正方形ABDE、ACGF,连接BE、FC、EF,并取BE、FC、EF、BC的中点I、J、H、K,连接IH、HJ、JK、IK,求证:HIKJ为正方形.
在任意三角形ABC边上画正方形ABDE、ACGF,连接BE、FC、EF,并取BE、FC、EF、BC的中点I、J、H、K,连接IH、HJ、JK、IK,求证:HIKJ为正方形.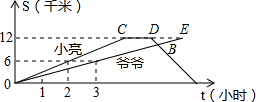 如图,表示的大刚与爷爷春游时,沿相同的路线同时从山脚下出发到达山顶的过程中,各自行进的路程随时间变化的图象.请你根据图象提供的信息解答下列问题:
如图,表示的大刚与爷爷春游时,沿相同的路线同时从山脚下出发到达山顶的过程中,各自行进的路程随时间变化的图象.请你根据图象提供的信息解答下列问题: 如图,均匀的正四面体的各面依次标有1,2,3,4四个数.
如图,均匀的正四面体的各面依次标有1,2,3,4四个数.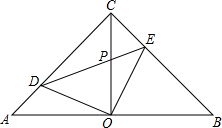 如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:
如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论: