Question

【题目】已知：如图1，点、、依次在直线上，现将射线绕点沿顺时针方向以每秒的速度旋转，同时射线绕点沿逆时针方向以每秒的速度旋转，如图，设旋转时间为（秒秒）.

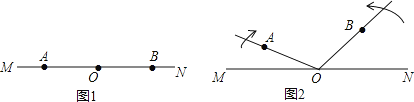
（1）用含的代数式表示的度数.

（2）在运动过程中，当第二次达到时，求的值.

（3）在旋转过程中是否存在这样的，使得射线是由射线、射线、射线中的其中两条组成的角（指大于而不超过的角）的平分线？如果存在，请直接写出的值；如果不存在，请说明理由.

Answer 1

【答案】（1）∠MOA=2t；（2）40秒；（3）t的值分别为18、22.5、36、67.5秒.

【解析】

（1）∠AOM的度数等于OA旋转速度乘以旋转时间；

（2）当∠AOB第二次达到60°时，射线OB在OA的左侧，根据∠AOM+∠BON-∠MON=60°列方程求解可得；

（3）射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线有三种情况：

①OB平分∠AOM时，根据∠AOM=∠BOM，列方程求解，

②OB平分∠MON时，根据∠BOM=∠MON，列方程求解，

③OB平分∠AON时，根据∠BON=∠AON，列方程求解．

（1）由题意得：∠MOA=2t；

（2）如图，

根据题意知：∠AOM=2t，∠BON=4t，

当∠AOB第二次达到60°时，∠AOM+∠BON-∠MON=60°，

即2t+4t-180=60，解得：t=40，

故t=40秒时，∠AOB第二次达到60°；

（3）射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线有以下三种情况：

①OB平分∠AOM时，

∵∠AOM=∠BOM，

∴t=180-4t，

解得：t=36；

②OB平分∠MON时，

∵∠BOM=∠MON，即∠BOM=90°，

∴4t=90，或4t-180=90，

解得：t=22.5，或t=67.5；

③OB平分∠AON时，

∵∠BON=∠AON，

∴4t=（180-2t），

解得：t=18；

综上，当t的值分别为18、22.5、36、67.5秒时，射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线．