题目内容
10．已知直角三角形的三边，b，c，且两直角边a，b满足等式（a2+b2）2-2（a2+b2）-15=0，求斜边c的值．分析 先由勾股定理得出a2+b2=c2，再将这个等式代入a2+b2）2-2（a2+b2）-15=0，解方程求出c2的值，然后求其算术平方根即可．
解答 解：设这个直角三角形的斜边长是c．
∵a，b分别是一个直角三角形的两直角边的长，
∴a2+b2=c2，
又∵（a2+b2）2-2（a2+b2）-15=0，
∴（c2）2-2c2-15=0，
∴（c2-5）（c2+3）=0，
∵c2＞0，
∴c2=5，
∵c＞0，
∴c=$\sqrt{5}$．
即这个直角三角形的斜边长是$\sqrt{5}$．
点评 本题考查了勾股定理及一元二次方程的应用，难度中等，将由勾股定理得到的等式a2+b2=c2，代入已知条件得出一个关于c2的一元二次方程，是解题的关键．
练习册系列答案
相关题目
4．抛物线y=-2x2+1的对称轴是（ ）
| A． | 直线$x=\frac{1}{4}$ | B． | 直线$x=-\frac{1}{4}$ | C． | y轴 | D． | x轴 |
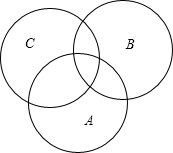已知有三个数集：A={-1，-3.1，-4，6，2.1}，B={-4，2，2.1，-1，10，-$\frac{1}{8}$}，C={2.1，-4.2，8，6}