题目内容
 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上,AF=40m,AE=30m.
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上,AF=40m,AE=30m.(1)如果设矩形的一边AB=x m,那么AD边的长度如何表示?
(2)设矩形的面积为y m2,当x取何值时,y的值最大?最大值是多少?
分析:(1)由矩形的性质可知:DC∥AF,所以△EDC∽△EAF,相似三角形的性质:对应边的比值相等即可得到AD和AB的关系,
(2)利用(1)中的关系式进而可表示出矩形面积,再利用配方法,求出最大值即可.
(2)利用(1)中的关系式进而可表示出矩形面积,再利用配方法,求出最大值即可.
解答:(1)解:∵四边形ABCD是矩形,
∴AB=DC,DC∥AF,
∵AF=40m,AE=30m,AB=xm,
∴CD=xm,
∵CD∥AF,
∴△EDC∽△EAF,
∴
=
,
∴
=
,
∴DE=
x,
∴AD=30-
x;
(2)∵矩形铁皮的面积:
y=AD×AB=x×(30-
x)=-
(x-20)2+300(0<x<40),
∴x=20时,最大面积y为300m2.
∴AB=DC,DC∥AF,
∵AF=40m,AE=30m,AB=xm,
∴CD=xm,
∵CD∥AF,
∴△EDC∽△EAF,
∴
| CD |
| AF |
| ED |
| AE |
∴
| x |
| 40 |
| DE |
| 30 |
∴DE=
| 3 |
| 4 |
∴AD=30-
| 3 |
| 4 |
(2)∵矩形铁皮的面积:
y=AD×AB=x×(30-
| 3 |
| 4 |
| 3 |
| 4 |
∴x=20时,最大面积y为300m2.
点评:本题考查了二次函数模型的构建以及相似三角形的性质与判定等知识,解题的关键是构建二次函数模型,利用配方法求函数的最值.

练习册系列答案
相关题目
教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:

(1)sad 的值为( ▼ )
的值为( ▼ )
(2)对于 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .
(3)已知 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A=
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题:

(1)sad
 的值为( ▼ )
的值为( ▼ )A. | B.1 | C. | D.2 |
 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .(3)已知
 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值. 教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad  的值为( ▼ )
的值为( ▼ )
A. | B.1 | C. | D.2 |
 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .(3)已知
 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值. 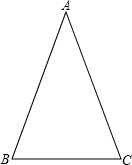 互唯一确定的.
互唯一确定的. .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
 的值为( ▼ )
的值为( ▼ ) B.
1 C.
B.
1 C.  D.
2
D.
2 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ . ,其中
,其中 为锐角,试求sad
为锐角,试求sad