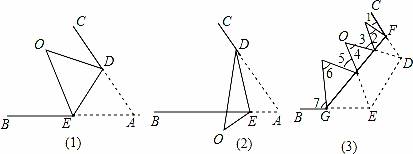
题目内容
如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠GDF＝∠ADF．
(1)求证：△ADE≌△BFE；
(2)连接EG，判断EG与DF的位置关系并说明理由．
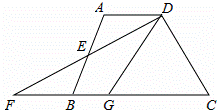
（1）证明：∵AD∥BC ∴∠ADE=∠F
∵E是AB的中点 ∴AE=BE
∴△ADE≌△BFE（ASA）（也可以AAS）
（2）EG与DF的位置关系是EG⊥DF
理由：∵∠GDF=∠ADE ∠ADE=∠BFE
∴∠GDF=∠BFE
又∵由（1）△AED≌△BFE得：DE=EF，即GE为DF上的中线，
∴GE⊥DF
练习册系列答案
相关题目
− 2的值等
于 。
如图，下列汉字中近似为轴对称图形的有（ ）
|
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
下列图形中对称轴最多的是（ ）
|
| A． | 圆 | B． | 正方形 | C． | 等腰三角形 | D． | 线段 |
