题目内容
2.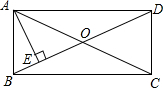 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=22.5度.
如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=22.5度.
分析 首先证明△AEO是等腰直角三角形,求出∠OAB,∠OAE即可.
解答 解: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,
∴OA=OB═OC,
∴∠OAD=∠ODA,∠OAB=∠OBA,
∴∠AOE=∠OAD+∠ODA=2∠OAD,
∵∠EAC=2∠CAD,
∴∠EAO=∠AOE,
∵AE⊥BD,
∴∠AEO=90°,
∴∠AOE=45°,
∴∠OAB=∠OBA=$\frac{180°-45°}{2}$=67.5°,
∴∠BAE=∠OAB-∠OAE=22.5°.
故答案为22.5°.
点评 本题考查矩形的性质、等腰直角三角形的性质等知识,解题的关键是发现△AEO是等腰直角三角形这个突破口,属于中考常考题型.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
10.三角形的内角和等于( )
| A. | 90° | B. | 180° | C. | 300° | D. | 360° |
17.(-2)3=( )
| A. | -6 | B. | 6 | C. | -8 | D. | 8 |
7.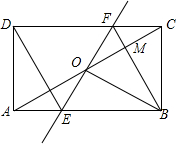 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )
 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
14.若一个几何体的主视图、左视图、俯视图是半径相等的圆,则这个几何体是( )
| A. | 圆柱 | B. | 圆锥 | C. | 球 | D. | 正方体 |
4.将根号外的式子移到根号内:m$\sqrt{-\frac{1}{m}}$=( )
| A. | $\sqrt{-m}$ | B. | -$\sqrt{m}$ | C. | -$\sqrt{-m}$ | D. | 1 |
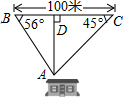 如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为60米.(sin56°≈0.8,tan56°≈1.5)
如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为60米.(sin56°≈0.8,tan56°≈1.5)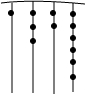 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )