题目内容
10.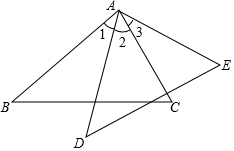 如图,∠1=∠3,∠B=∠D,AB=DE=5,BC=4,
如图,∠1=∠3,∠B=∠D,AB=DE=5,BC=4,(1)请证明△ABC∽△ADE.
(2)求AD的长.
分析 (1)由∠1=∠3,推出∠1+∠2=∠3+∠2,即∠BAC=∠DAE,由∠B=∠D,即可根据两角对应相等的两个三角形相似进行证明.
(2)利用相似三角形的性质即可解决问题.
解答 (1)证明:∵∠1=∠3,
∴∠1+∠2=∠3+∠2,
即∠BAC=∠DAE,∵∠B=∠D,
∴△BAC∽△DAE.
(2)∵△BAC∽△DAE,
∴$\frac{AB}{AD}$=$\frac{CB}{DE}$,
∵AB=DE=5,BC=4,
∴$\frac{5}{AD}$=$\frac{4}{5}$,
∴AD=$\frac{25}{4}$.
点评 本题考查相似三角形的判定和性质,等式的性质等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于基础题,中考常考题型.

练习册系列答案
相关题目
20.一种商品原价200元,由于市场情况不好,经过连续两次降价m%后售价为148元,则下面所列方程中正确的是( )
| A. | 200(1+m%)2=148 | B. | 200(1-m%)2=148 | C. | 200(1-2m%)2=148 | D. | 200[1-(m%)2]=148 |
19.如果ab<0,a+b>0,那么这两个有理数a,b为( )
| A. | 绝对值相等的数 | |
| B. | 符号不同的数,其中正数的绝对值较大 | |
| C. | 符号不同的数,其中负数的绝对值较大 | |
| D. | 以上都不正确 |

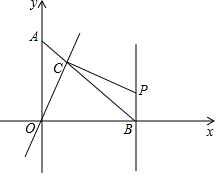 如图,点A(0,a ),点B( b,0 )且满足a2+2b2-2ab-2b+1=0.经过原点O的直线l交线段AB于点C,过C作OC⊥CP,与直线BP相交于点P,BP⊥OB.现将直线l绕O点旋转,使交点C从A向B运动,但P点必须在第一象限内,分析此图后,对下列问题作出探究:
如图,点A(0,a ),点B( b,0 )且满足a2+2b2-2ab-2b+1=0.经过原点O的直线l交线段AB于点C,过C作OC⊥CP,与直线BP相交于点P,BP⊥OB.现将直线l绕O点旋转,使交点C从A向B运动,但P点必须在第一象限内,分析此图后,对下列问题作出探究: 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料.