题目内容
某市出租车按里程计费标准为:不超过3公里部分,计费11元,超过3公里部分,按每公里2.4元计费.现在在此基础上,如果车速不超过12公里/小时,那么再加收0.48元/分钟,这项费用叫做“双计费”.图中三段折线表示某时间段内,一辆 出租车的计费总额y(元)与行驶时间x(分钟)的函数关系(出租车在每段上均匀速行驶).
出租车的计费总额y(元)与行驶时间x(分钟)的函数关系(出租车在每段上均匀速行驶).
(1)写出AB段表示的实际意义;
(2)求出线段BC所表示的y与x的函数关系式;
 (3)是否可以确定在CD段该辆出租车的计费过程中产生了“双计费”的费用?请说明你的理由.
(3)是否可以确定在CD段该辆出租车的计费过程中产生了“双计费”的费用?请说明你的理由.
解:(1)出租车行驶了6 分钟,不超过3公里,收费11元.
(2)设当6≤x≤11时,y与x的函数关系式为y=kx+b.
由图象,当x=6时,y=11,当x=11时,y=17.
 解得:
解得:
∴y与x的函数关系式为:y=1.2x+3.8.
(3)不能确定.
①若产生了“双计费”,5分钟费用增加5×0.48=2.4(元),出租车在第11到16分钟以12公里/小时的速度,行驶了 ×5=1(千米),费用增加2
×5=1(千米),费用增加2 .4元,车费总额增加4.8元,符合题意.
.4元,车费总额增加4.8元,符合题意.
②若没有产生“双计费”,出租车在第11到16分钟以24公里/小时的速度,5分钟行驶了2千米,费用增加2×2.4=4.8(元),符合题意.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 .
. ,
, )
)

 B.y=
B.y= C.y=
C.y= D.y=
D.y=
 的解是 .
的解是 . ②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
 ,一边长为
,一边长为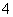 ,则它的另两边长为 .
,则它的另两边长为 .