题目内容
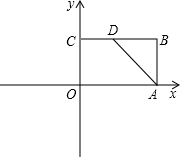 如图,矩形OABC的顶点B点坐标为(3,2),点D是BC的中点.
如图,矩形OABC的顶点B点坐标为(3,2),点D是BC的中点.(1)将△ABD向左平移3个单位,则点D的对应点E的坐标为
(-
,0)
| 3 |
| 2 |
(-
,0)
;| 3 |
| 2 |
(2)若点E在双曲线y=
| k |
| x |
-3
-3
,直线OE与双曲线的另一个交点F的坐标是(
,-2)
| 3 |
| 2 |
(
,-2)
;| 3 |
| 2 |
(3)若在y轴上有一动点P,当点P运动到何处时PB+PF的值最小?求出此时的P点坐标.
分析:(1)根据矩形的性质和点D是BC的中点可得到点D坐标为(
,2),再利用平移的性质即可得到点D的对应点E的坐标为(
-3,2);
(2)把E(-
,2)代入y=
即可得到k=-3,然后根据正比例函数图象与双曲线的两个交点关于原点中心对称得到点F的坐标为(
,-2);
(3)作点F关于y轴的对称点F′,连BF′交y轴于点P,则PF=PF′,利用两点之间线段最短得到此时点P使PB+PF的值最小,再利用关于y轴对称的坐标特点得到点F′的坐标为(-
,-2),然后利用待定系数法可确定直线BF的解析式y=
x-
,则得到P点坐标为(0,-
).
| 3 |
| 2 |
| 3 |
| 2 |
(2)把E(-
| 3 |
| 2 |
| k |
| x |
| 3 |
| 2 |
(3)作点F关于y轴的对称点F′,连BF′交y轴于点P,则PF=PF′,利用两点之间线段最短得到此时点P使PB+PF的值最小,再利用关于y轴对称的坐标特点得到点F′的坐标为(-
| 3 |
| 2 |
| 8 |
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:(1)∵矩形OABC的顶点B点坐标为(3,2),点D是BC的中点,
∴点D坐标为(
,2),
当将△ABD向左平移3个单位,即点D向左平移3个单位,
∴点D的对应点E的坐标为(
-3,2),即E(-
,2);
(2)把E(-
,2)代入y=
得k=-
×2=-3
∵直线OE为正比例函数图象,
∴直线OE与双曲线的两个交点关于原点中心对称,
∴点F的坐标为(
,-2).
故答案为(-
,2);-3,(
,-2);
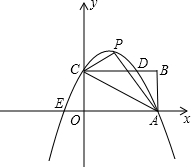
(3)作点F关于y轴的对称点F′,连BF′交y轴于点P,如图,
则PF=PF′,
∴PB+PF=PB+PF′=BF′
∵两点之间线段最短,
∴此时点P使PB+PF的值最小,
∵点F的坐标为(
,-2);
∴点F′的坐标为(-
,-2),
设直线BF′的解析式为y=kx+b(k≠0),
把B(3,2)、F′(-
,-2)代入得
,
解得
,
∴直线BF的解析式y=
x-
,
∴P点坐标为(0,-
,).

∴点D坐标为(
| 3 |
| 2 |
当将△ABD向左平移3个单位,即点D向左平移3个单位,
∴点D的对应点E的坐标为(
| 3 |
| 2 |
| 3 |
| 2 |
(2)把E(-
| 3 |
| 2 |
| k |
| x |
| 3 |
| 2 |
∵直线OE为正比例函数图象,
∴直线OE与双曲线的两个交点关于原点中心对称,
∴点F的坐标为(
| 3 |
| 2 |
故答案为(-
| 3 |
| 2 |
| 3 |
| 2 |
(3)作点F关于y轴的对称点F′,连BF′交y轴于点P,如图,
则PF=PF′,
∴PB+PF=PB+PF′=BF′
∵两点之间线段最短,
∴此时点P使PB+PF的值最小,
∵点F的坐标为(
| 3 |
| 2 |
∴点F′的坐标为(-
| 3 |
| 2 |
设直线BF′的解析式为y=kx+b(k≠0),
把B(3,2)、F′(-
| 3 |
| 2 |
|
解得
|
∴直线BF的解析式y=
| 8 |
| 9 |
| 2 |
| 3 |
∴P点坐标为(0,-
| 2 |
| 3 |
点评:本题考查了反比例函数的综合题:理解反比例函数图象关于原点中心对称;掌握待定系数法确定函数的解析式;熟练运用两点关于坐标轴对称的坐标特点、平移的性质和两点之间线段最短.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA= (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是