题目内容
【题目】我们知道,解一元二次方程,可以把它转化为两个一元一次方程来解,其实用“转化”的数学思想我们还可以解一些新的方程例如一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,通过解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.
(1)方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= .
(2)用“转化”的思想求方程![]() =x的解.
=x的解.
(3)试直接写出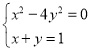 的解 .
的解 .
【答案】(1)1,2;(2)3;(3)![]() ,
,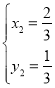 .
.
【解析】
(1)根据题意对方程![]() 进行因式分解即可求出
进行因式分解即可求出![]() 的值.
的值.
(2)先把等号左右两边同时平方,去掉根号,然后进行因式分解即可.
(3)将![]() 用平方差公式拆成
用平方差公式拆成![]() 与
与![]() 组成两个二元一次方程组,解方程组即可.
组成两个二元一次方程组,解方程组即可.
解:(1)∵x3+x2﹣2x=0
∴x(x2+x﹣2)=0,
∴x(x﹣1)(x+2)=0
则x=0或x﹣1=0或x+2=0
解得x1=0,x2=1,x3=﹣2,
故答案为1,2;
(2)∵![]() =x,
=x,
∴2x+3=x2(x≥0),即x2﹣2x﹣3=0,
∴(x+1)(x﹣3)=0
则x+1=0或x﹣3=0,
解得x1=﹣1(舍去,不合题意),x2=3.
(3)∵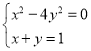 ,
,
∴![]() 或
或![]() ,
,
解得![]() ,
,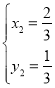 .
.
故答案为![]() ,
,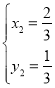 .
.

练习册系列答案
相关题目