题目内容
4.下列说法:①若|x|+x=0,则x为负数;②若-a不是负数,则a为非正数;③|-a2|=(-a)2; ④若$\frac{a}{|a|}$$+\frac{b}{|b|}$=0,则$\frac{ab}{|ab|}$=-1;其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据绝对值的性质:正数的绝对值等于它本身,负数的绝对值是它的相反数,0的绝对值是0,即可判断.
解答 解:①若|x|+x=0,则x为负数或0,故错误;
②若-a不是负数,则a为非正数,正确;
③|-a2|=(-a)2;,正确;
④若$\frac{a}{|a|}$$+\frac{b}{|b|}$=0,则$\frac{ab}{|ab|}$=-1,正确;
正确的有3个,
故选:B.
点评 本题考查了绝对值,解决本题的关键是熟记正数的绝对值等于它本身,负数的绝对值是它的相反数,0的绝对值是0.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
15.在Rt△ABC中,∠C=90°,点D为斜边AB上的中点,CD=3,那么AB为( )
| A. | 1.5 | B. | 6 | C. | 3 | D. | 12 |
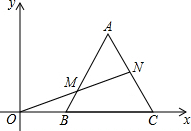 如图,在平面直角坐标系中,等边三角形ABC的顶点B、C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M.当边AB恰平分线段ON时,则AN=2.
如图,在平面直角坐标系中,等边三角形ABC的顶点B、C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M.当边AB恰平分线段ON时,则AN=2.

